2018学年上海闵行区文莱中学初二（下）第二次月考
数学测试题
1、一次函数y=-2在y轴上的截距是..
2 -3 6 6
2,下列方程中,有实数解的方程的是.....
3,顺次联结对角线互相垂直的等腰梯形各边中点所得的四边形是…
平行四边形 矩形 菱形 正方形
4,下列事件: ①蜡烛在没氧气的瓶中燃烧: ②掷一枚普通的骰子，朝上一面的点数低于6: ③掷两枚质地均匀的正方体骰子，朝上一面的点数之和大于6④两个非零实数的积为正数.是确定事件的个数是
1个 2个 3个 4个
下列各式中错误的是……
6.下列命题是假命题的是...
对角线互相垂直且相等的平行四边形是正方形 对角线互相垂直的矩形是正方形 对角线相等的菱形是正方形 对角线互相垂直的四边形是正方形
2、填空题
7，一次函数y=3x-5的图像不经过第__________象限。
8,经过点且与直线y=-5x+1平行的直线的表达式是__________ ______________________________________
9.已知一次函数y=x+m-1,当y的值伴随x的值增大而减小时,则实数m的取值范围是______________________________________
10.方程
的根是______________________________________
11、.解方程 
时,设y=
,那样原方程可化为关于y的整式方程为______________________________________
12,在一个不透明的布袋中有若干个除颜色外形状大小相同的小球,假如其中有2个白球, n个黄球,从中随机摸出白球的概率是
,那样n=______________________________________
13,若一个凸多边形的内角和是它的外角和的3倍,则这个多边形的边数是____________________________
14,在
ABC中, M , N分别是AB. AC的中点,且
,则∠ANM=___________________________度.
15,已知一个菱形的面积是
',其中一条对角线长为4cm,则这个菱形的另一条对角线长为 ________________
已知矩形ABCD的两条对角线相交于点O, BO=2, BC=3,则 
__________________
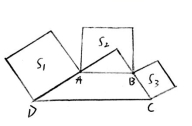
如图,在梯形ABCD中, AB// DC, ∠ADC+ ∠BCD=90°,且DC=2AB,分别以DA AB,BC为边向梯形外作正方形,其面积分别为
，
,
则，,之间的关系是__________________
18如图，梯形ABCD中, AD// BC, ∠B=90°, AD=2, BC=5,E是AB上一点，将△BCE沿着直线CE翻折,点B恰好与点D重合,则BE=__________________
3、解答卷
19.
解方程:
20.
解方程组:
21.
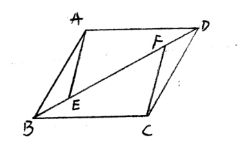
如图，已知：在平行四边形ABCD中，点E、F在对角线BD上，且BE=DF
在图中画出向量
的差向量并填空:
=
图中与平行的向量是:
若,用
=
22. 有一个不透明的袋子里装有除标记数字不同外其余都相同的4个小球,小球上的数字分别标有2、3、4、6
任意摸出一个小球,所标的数字超越5的概率是
任意摸出两个小球,所标的数字积是奇数的概率是
任意摸出一个小球,记下所标的数字后,再将小球放回袋中,搅匀后再摸出一个小球,摸到的这两个小球所标数字的和为偶数的概率是多少?
23, 小题3分,第小题5分)
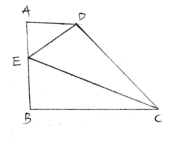
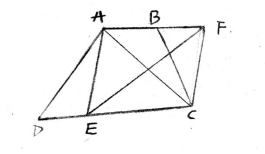
如图,已知四边形ABCD中,点E是CD上的点, DE=AB, ∠BAC=∠D，AD=AC
求证:四边形AECB是等腰梯形；
点F 是AB 边延长线上一点，且BC=CF .联结CF、EF,若AC⊥EF求证：四边形AECF是菱形.
24.
为庆祝“六”活动,镇活动中心需要600个环保纸袋,原计划由初中二年级班全体同学制作完成、在实质制作时,又有初中二年级班10名同学自愿加入参与制作,如此,实质参加制作的同学人均制作的数目比原计划少5个,原么初中二年级班共有多少名同学?
小题2分,第小题4分,第小题2分)
已知:直线
经过点A且与直线
: y=-x+6平行,直线
与x轴、y轴分别交于点B，C
求直线的表达式及其与x轴的交点D的坐标:
判断四边形ABCD是什么四边形?并证明你的结论:
若点E是直线AB上一点,平面内存在一点F,使得四边形CBEF是正方形,求点E的坐标. 请直接写出答案.
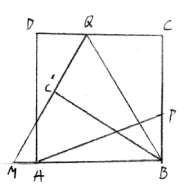
小题3分,第小题4分,第小题3分如图,P为正方形ABD的边BC上一动点,联结AP,过点B作BQ⊥AP交CD于点Q,将△BQC沿所在的直线对折得到△BQC’,延长QC’交BA的延长线于M点 试探究AP与BQ的数目关系,并证明你的结论:
当AB=3,BP=2PC,求QM的长；
13)当BP=m,PC =n时.求AM的长
