第一学期交大附中八上《一次函数》单元测试
班级__________名__________号__________
1、选择题
1．下列函数（1）y＝πx；y＝2x－1； 
；
中，
是一次函数的有（ ）
A．4个 B．3个 C．2个 D．1个
2．直线y=2x－4与y轴的交点坐标是
A． B． C． D．
3．关于一次函数y=－2x＋4，下列结论错误的是
A．函数值随自变量的增大而减小
B．函数的图像不经过第三象限
C．函数的图像向下平移4个单位长度得y=－2x的图像
D．函数的图像与x轴的交点坐标是
4．函数
中，自变量x的取值范围是（ ）
A．x≥1 B．x＞1 C．x≥1且x≠2 D．x≠2
5. 若函数
（m为常数）是正比率函数，则m的值为（ ）
A.
B.
C.
D.
6．设正比率函数y=m x的图像经过点A ，且y的值随x值的增大而减小，则m的
值为
A．2 B．－2 C．4 D．－4
7．将直线y=2x 向右平移1个单位长度后所得图像对应的函数分析式为
A．y=2x－1 B．y=2x－2 C．y=2x＋1 D．y=2x＋2
8．若正比率函数的图像经过点（－1，2），则这个图像必经过点（ ）
A． B． C． D．
10.已知一次函数y=kx+b的图象如图，则k、b的符号是（）
A．k＞0，b＞0 B．k＞0，b＜0
C．k＜0，b＞0 D．k＜0，b＜0
11．已知点A（a+2，5）、B（﹣4，1﹣2a），若AB平行于x轴，则a的值为（）
A．-6 B．2 C．3 D．-2
12．如图，若一次函数
的图像l1与
的图
像交于点P，则方程组的解是
A．
B．
C． D．
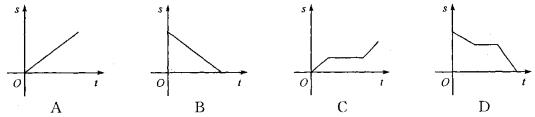
13．小明骑自行车上学，开始以正常速度匀速行驶，但行至中途自行车出了问题，只好停
下来修理汽车，车修好后，因怕耽误上课，加快了骑行车速度度．下面是小明离家后他到学校剩下
的路程s关于时间t的函数图像，其中符合小明行驶状况的图像大致是
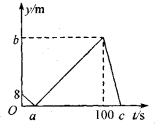
14．甲、乙两人在直线跑道上同起点、同终点、同方向匀 速跑步500m，先到终点的人原地休息．已知甲先出发2 s．在跑步过程中，甲、乙两人的距离y 与乙出发的时间t 之间的关系如图所示．给出以下结论：①a=8；②b=92；③c=123．其中正确的是
A．①②③ B．仅有①②
C．仅有①③ D．仅有②③
15、直线与y=x-1与两坐标轴分别交于A、B两点，点C在坐标轴上，若△ABC为等腰三角形，则满足条件的点C最多有（ ）.
A．4个 B．5个 C．6个 D．7个
2、填空题
16．点A（﹣1，y1），B（3，y2）是直线y=kx+b（k＜0）上的两点，则y1﹣y2__________0
17．求直线y=x＋6与坐标轴围成的三角形的面积为__________ ．
18．与直线y=2x+1关于x轴对称的直线的分析式是__________．
19．如图，一个正比率函数的图像与一次函数y=－x＋1的图像相交于点P，则这个正比率函数的表达式是__________．
20．将直线y=2x﹣1向上平移2个单位，再向右平移1个单位后得到的直线为__________
21．无论a取什么实数，点P 都在直线l上．若Q 是直线l上的
点，则 2的值等于__________．__________
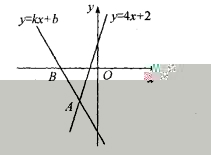
22．如图，已知经过点B 的直线y=kx＋b与直线y=4x＋2相交于点A ，则不等式4x＋2＜kx＋b＜0的解集为__________．
3、解答卷
23． 已知一次函数y=kx＋b，当x=0时，y的值为4；当x=－1时，y的值为－2．求这个一次函数的分析式．
26． 已知一次函数y=kx＋b 的图像过点 ，且与两坐标轴围成的三角形的面积为2，求此一次函数的分析式．
27． 某游泳池有水4000m3，现放水清洗池子．同时，员工记录放水的时间z 与池内水量y 的对应变化状况如下表所示：
依据上表提供的信息，当放水到第80min时，池内有水多少立方米?
请你用函数分析式表示y与x间的关系，并写源于变量x的取值范围．
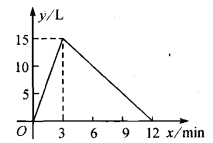
28. 一个有进水管与出水管的容器，从某时刻开始的3min内只进水不出水，在随后的9 min内既进水又出水，每分钟的进水量和出水量都是常数．容器内的水量y 与时间x 之间的关系如图所示．当容器内的水量大于5L时，求时间x的取值范围．
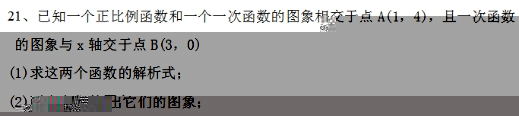
29、如图，在平面直角坐标系内，已知点A（0，6）、点B（8，0），动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动，同时动点Q从点B开始在线段BO上以每秒2个单位长度的速度向点O移动,设点P、Q移动的时间为t秒．
求直线AB的分析式； 当t为什么值时，△APQ的面积为
个平方单位
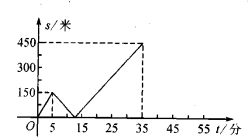
30． 甲、乙两人匀速从同一地址到相距1500米的图书馆看书，甲出发5分钟后，乙以50米／分的速度沿同一路线行走．设甲、乙两人相距s ，甲行走的时间为t ，s关于t的函数图像的一部分如图所示．
求甲行走的速度；
在坐标系中，补画s关于x的函数图像的其余部分；
问甲、乙两人何时相距360米?
31． 新农村社区改造中，有一部分楼盘要对外销售．某楼盘共23层，销价格格如下：第八层楼房价格为4000元／平米，从第八层起每上升一层，每平米的价格提升50元；反之，楼层每降低一层，每平米的价格减少30元，已知该楼盘每套楼房面积均为120平米．若购买者一次性付清所有房款，开发商有两种打折策略：
策略1、降价8％，另外每套楼房赠送a元装修基金；
策略2、’降价10％，没其他赠送．
请写价格y 与楼层x 之间的函数关系式；
老王要购买第十六层的一套楼房，若他一次性付清购房款，请帮他计算哪种打折策略愈加划算．
