直角三角形例题精讲与训练
【例题精讲】
例1 若a、b、c是直角三角形的三条边长，斜边c上的高的长是h，给出下列结论：①以a2，b2，c2的长为边的三条线段能组成一个三角形；②以
，
，
的长为边的三条线段能组成一个三角形；③以a+b，c+h，h的长为边的三条线段能组成直角三角形；④以
，，
，
的长为边的三条线段能组成直角三角形．其中所有正确结论的序号为______________．
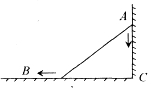
例2 如图，梯子AB斜靠在墙面上，AC⊥BC，AC=BC，当梯子的顶端A沿AC方向下滑x米时，梯足B沿CB方向滑动y米，则x与y的大小关系是（ ）．
A．x=y B．x>y C．x<y D．不确定
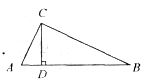
例3 如图，在
求证：（1）
；
（2）
；
（3）
为边的三角形是直角三角形．
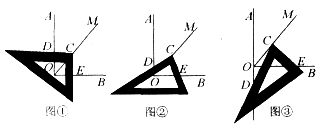
例4 已知∠AOB=90°，在∠AOB的平分线OM上有一点C，将一个三角板的直角顶点与C重合，它的两条直角边分别与OA、OB（或它们的反向延长线）相交于点D、E．
当三角板绕C旋转到CD与OA垂直时，如图①，易证OD+OE=
OC．当三角板绕点C旋转到CD与OA不垂直时，如图②、图③这两种状况下、上述结论是不是还成立？若成立，请给予证明；若不成立，线段OD、OE、OC之间又有什么样的数目关系？请写出你的猜想，不需证明．
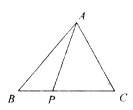
例5 如图，已知P为△ABC边BC上的一点．且PC=2PB，∠ABC=45°，∠APC=60°，求∠ACB的度数．
【实战演练】
用直角边分别为3和4的两个直角三角形拼成凸四边形．所得的四边形的周长是__________．
2．如图，P是正△ABC内的一点，且PA=6，PB=8，PC=10，若将△PAC绕点A旋转后，得到△P’AB，则点P与点P’ 之间的距离为____________，∠APB=____________．
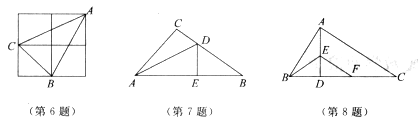
3．如图，已知AB=13，BC=14，AC=15，AD⊥BC于D，则AD=____________．
4．如图，在四边形ABCD中，AB、BC、CD、DA的长分别为2，2，
，2，并且AB⊥BC，则∠BAD的度数为____________．
5．如图，在△ABC中，AB=AC=5，BC=6，点M为BC的中点，MN⊥AC于点N，则MN等于（ ）．
A．
B． C．
D．
6．如图，小正方形边长为1，连接小正方形的三个顶点，可得△ABC，则AC边上的高为（ ）．
A．
B．
C． D．
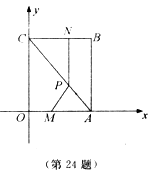
7．如图，有一张直角三角形纸片，两直角边AC=6cm，BC=8cm，将△ABC折叠．
使B点与A点重合，折痕为DE，则CD等于（ ）cm．
A． B．
C．
D．
8．如图,在Rt△ABC中，AB⊥AC，AD⊥BC，BE平分∠ABC，交AD于E，EF∥AC，下列结论肯定成立的是（ ）．
A．AB=BF B．AE=ED C．AD=DC D．∠ABE=∠
DFE
9．如图，已知△ABC和△ECD都是等腰直角三角形，∠ACB=∠DCE=90°，D为AB边上一点．求证：
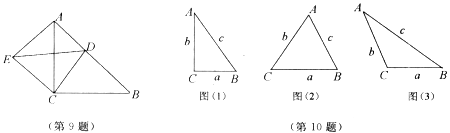
10．△ABC中，BC=a，AC=b，AB=c，若∠C=90°，如图（1），依据勾股定理，则a2+b2=c2，若△ABC不是直角三角形，如图（2）、（3），请你类比勾股定理，试猜想 a2+b2与c2的关系，并证明你的结论．
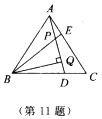
11．如图，在△ABC中，已知AB=BC=CA，AE=CD，AD、BE相交于P，BQ⊥AD于Q，求证：BP=2PQ．
12．漂亮的人造平面珊瑚礁图案．图中的三角形都是直角三角形，图中的四边形都是正方形，假如图中所有些正方形的面积之和是980平方厘米．问：最大的正方形的边长是___________．
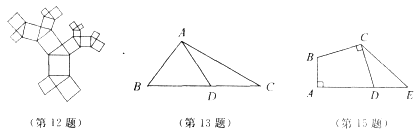
13．如图，在△ABC中，AB=5，AC=13，边BC上的中线AD=6，则BC的长为____________．
14．△ABC中，AC=BC，∠ACB=90°，D、E是AB上两点，AD=3，BE=4，∠DCE=45°，则△ABC的面积是____________．
15．如图，在四边形ABCD中，∠A=∠BCD=90°，BC=CD，E是AD延长线上一点，若DE=AB=3，CE=4在，则AD的长为____________．
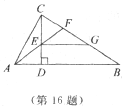
16．如图，Rt△ABC中，∠ACB=90°，CD⊥AB于D，AF平分∠CAB交CD于E，交CB于F，且EG∥AB交CB于G，则CF与GB的大小关系是（ ）．
A．CF>GB B．CF=GB C．CF<GB D．没办法确定
17．对如下的3个命题：
命题1：边长为连续整数的直角三角形是存在的．
命题2：边长为连续整数的锐角三角形是存在的．
命题3：边长为连续整数的钝角三角形是存在的．
正确命题的个数为（ ）．
A．0 B．1 C．2 D．3
18．2002年8月在北京召开的国际数学家大会会标取材于国内古时候数学家赵爽的《勾股圆方图》，它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形（如图所示）．假如大正方形的面积是13，小正方形的面积是1，直角三角形的较短直角边为a，较长直角边为b，那样（a+b）2的值为（ ）．
A．13 B．19 C．25 D．169
19．在锐角三角形中，已知某两边a=1，b=3，那样第三边的变化范围是（ ）．
A． B．
C．
D．
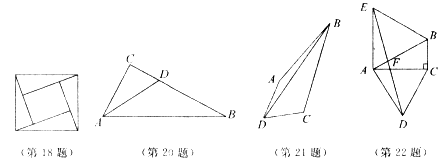
20．如图，已知∠ACB=90°，是∠CAB的平分线，BC=4，CD=，求AC的长．
21．如图，已知∠ABC=30°，∠ADC=60°，AD=DC．求证：BD2=AB2+BC2．
22．如图，在Rt△ABC中，∠C=90°，∠A=30°，分别以AB、AC为边在△ABC的外侧作等边△ABE和等边△ACD，DE与AB交于F，求证：EF=FD．
应用探究乐园
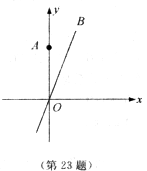
23．如图，直线OB是一次函数y=2x的图象，点A的坐标为（0，2），在直线OB上找点C，使得△ACO为等腰三角形，求点C的坐标．
24．如图，在平面直角坐标系中，四边形OABC为矩形，点A、B的坐标分别为（3，0）、（3，4），动点M、N分别从O、B同时出发，以每秒1个单位的速度运动，其中，点M从O点出发沿OA向终点A运动，点N从B出发沿BC向终点C运动，过点N作NP⊥BC，交AC于P．连MP，若M、N两动点运动了x秒．
（1）设△MPA面积为y，试求y与x的函数关系式；
（2）请你探索：当x为什么值时，△MPA是一个等腰三角形？
