初一(下)首次月考数学试题
1、选择题(共12小题,每小题3分,满分36分)
1.(3分)下列不是具备相反意义的量是()
A.前进5米和后退5米
B.收入30元和支出10元
C.向东走10米和向北走10米
D.超越5克和不足2克
2.(3分)将一个直角三角形绕它的最长边(斜边)旋转一周得到的几何体为()
A.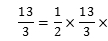 B.
B.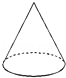 C.
C.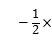 D.
D.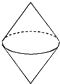
3.(3分)已知关于x的一元一次方程![]() x+3=2x+b的解为x=﹣2,那样关于y的一元一次方程
x+3=2x+b的解为x=﹣2,那样关于y的一元一次方程![]() (y+1)+3=2(y+1)+b的解为()
(y+1)+3=2(y+1)+b的解为()
A.y=3 B.y=1 C.y=﹣1 D.y=﹣3
4.(3分)如图,∠1和∠2是同位角的图形有()
A.1个 B.2个 C.3个 D.4个
5.(3分)![]() 的小数部分是()
的小数部分是()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.(3分)若m•n≠0,则![]() 的取值不可能是()
的取值不可能是()
A.0 B.1 C.2 D.﹣2
7.(3分)给出下列四个命题,其中真命题的个数为()
①坐标平面内的点可以用有序数对来表示;
②若a>0,b不大于0,则P(﹣a,b)在第三象限内;
③在x轴上的点,其纵坐标都为0;
④当m≠0时,点P(m2,﹣m)在第四象限内.
A.1 B.2 C.3 D.4
8.(3分)下列方程:①2x﹣3y=5;②xy=3;④x![]() 3;④3x﹣2y+z=0;⑤x2+y=6.其中,二元一次方程有()个.
3;④3x﹣2y+z=0;⑤x2+y=6.其中,二元一次方程有()个.
A.1 B.2 C.3 D.4
9.(3分)已知点P(x,y),且xy>0,点P到x轴的距离是3个单位,到y轴的距离是2个单位,则点P的坐标是()
A.(2,3) B.(3,2)
C.(2,3)或(﹣2,﹣3) D.(﹣3,﹣2)
10.(3分)若(a+2)x|a|﹣1﹣(b﹣1)y![]() 7是关于x、y的二元一次方程,则a、b的值分别是()
7是关于x、y的二元一次方程,则a、b的值分别是()
A.a=﹣2,b=﹣1 B.a=﹣2,b=1 C.a=2,b=1 D.a=2,b=﹣1
11.(3分)有甲、乙、丙三种货物,若购甲3件,乙7件丙1件,共需64元,若购甲4件,乙10件,丙1件,共需79元.现购甲、乙、丙各一件,共需()元.
A.32 B.33 C.34 D.35
12.(3分)如图,在平面直角坐标系中,A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),把一条长为2016个单位长度且没弹性的细线(线的粗细忽视不计)的一端固定在点A处,并按A→B→C→D→A…的规律绕在四边形ABCD的边上,则细线另一端所在地方的点的坐标是()

A.(﹣1,0) B.(1,﹣2) C.(1,1) D.(0,﹣2)
2、填空题(共6小题,每小题3分,满分18分)
13.(3分)计算2(4a﹣5b)﹣(3a﹣2b)的结果为__________.
14.(3分)已知![]() 是二元一次方程组
是二元一次方程组![]() 的解,则m+3n的立方根为__________.
的解,则m+3n的立方根为__________.
15.(3分)已知x与y互为相反数,m与n为倒数,且|a|=3,则(x+y)![]() __________.
__________.
16.(3分)如图是一个运算程序,若输入x的值为8,输出的结果是m,若输入x的值为3,输出的结果是n,则m﹣2n=__________.
17.(3分)已知实数x,y,z满足关系式(x﹣4)2![]() ,则代数式(5x+3y﹣3z)2019的末位数字是__________.
,则代数式(5x+3y﹣3z)2019的末位数字是__________.
18.(3分)已知x,y,z,a,b均为非零实数,且满足![]() ,则a的值为__________.
,则a的值为__________.
3、解答卷(共9小题,满分66分)
19.(6分)解方程组:
(1)![]()
(2) .
.
20.(6分)计算:
(1)﹣22×0.5﹣(![]() )2÷(﹣4)2
)2÷(﹣4)2
(2)![]()
21.(6分)国内古时候数学著作《九章算术》的“方程”一章里,一次方程组是由算筹布置而成的.如图1,图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项,把图1所示的算筹图用大家目前所熟知的方程组的形式表述出来,就是![]() 请你依据图2所示的算筹图,列出方程组,并求解.
请你依据图2所示的算筹图,列出方程组,并求解.
22.(7分)在平面直角坐标系中,有点A(﹣2,a+3),B(b,b﹣3).
(1)当点A在第二象限的角平分线上时,求a的值;
(2)当点B到x轴的距离是它到y轴的距离2倍时,求点B所在的象限地方.
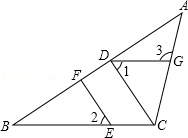
23.(7分)如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F,∠1=∠2.
(1)试说明DG∥BC的原因;
(2)假如∠B=54°,且∠ACD=35°,求的∠3度数.
24.(8分)2017年5月14日至15日,“一带一路”国际合作高峰平台在北京举行,本届平台期间,中国同30多个国家签署经贸合作协议,某厂筹备生产甲、乙两种产品共6万件销往“一带一路”沿线国家和区域,已知2件甲种产品与3件乙种产品的销售收入相同,3件甲种产品比2件乙种产品的销售收入多1500元.
(1)甲种产品与乙种产品的销售单价各多少元?
(2)若甲、乙两种产品的销售总收入高于4400万元,则至少销售甲种产品多少万件?
25.(8分)在平面直角坐标系中,A(6,a),B(b,0),M(0,c).p点为y轴上一动点,且(b﹣2)2+|a﹣6|![]() 0.
0.
(1)求点B、M的坐标;
(2)不论P点运动到直线OM上的任何地方(不包含点O、M),∠PAM、∠APB、∠PBO三者之间是不是都存在某种固定的数目关系,假如有,请借助所学常识找出并证明;假如没,请说明理由.
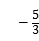
26.(9分)很多代数恒等式可以借用图形的面积关系直观表达,如图①,依据图中面积关系可以得到:(2m+n)(m+n)=2m2+3mn+n2

(1)如图②,依据图中面积关系,写出一个关于m、n的等式__________;
(2)借助(1)中的等式求解:a﹣b=2,ab![]() ,则(a+b)2=__________;
,则(a+b)2=__________;
(3)小明用8个面积一样大的长方形(宽a,长b)拼图拼出了如图甲、乙的两种图案:图案甲是一个大的正方形,中间的阴影部分是边长为3的小正方形;图案乙是一个大的长方形,求a,b的值.
27.(9分)在平面直角坐标系中,点O是坐标原点,点A的坐标是(﹣a,a)(0<a<5),点B的坐标是(1,b),点C的坐标是(c,0),且满足![]() .
.
(1)请用含a的代数式分别表示b和c.
(2)若S△ABC+S△AOB=S四边形OABC,求直线AB与y轴的交点N的纵坐标.
(3)在(2)的首要条件下,能否在坐标轴上找到一点M,使得S△MAB=S△MBC,若能,请求出满足条件的所有点M的坐标;若不可以,说明理由.
初一(下)首次月考数学试题
参考答案
1、选择题(共12小题,每小题3分,满分36分)
1.C; 2.D; 3.D; 4.C; 5.D; 6.B; 7.B; 8.A; 9.C; 10.D; 11.C; 12.D;
2、填空题(共6小题,每小题3分,满分18分)
13.__________; 14.__________; 15.__________; 16.__________; 17.__________; 18.__________;
3、解答卷(共9小题,满分66分)
19.解:(1)方程组的解为:![]() ;
;
(2)原方程组的解是: .
.
20.解:(1)﹣22×0.5﹣(![]() )2÷(﹣4)2
)2÷(﹣4)2
=﹣4×0.5![]() 16
16
=﹣2![]()
=﹣2![]() ;
;
(2)![]()
![]() (
(![]() )
)
![]() .
.
21.方程组的解是 ![]() .
.
22.解:(1)由题意,得a+3=2,
解得a=﹣1;
(2)由题意,得|b﹣3|=2|b|,
解得b=﹣3或b=1,
当b=﹣3时,点B(﹣3,﹣6)在第三象限,
当b=1时,点B(1,﹣2)在第四象限.
23.(1)证明:∵CD⊥AB,EF⊥AB,
∴CD∥EF,
∴∠2=∠BCD.
又∵∠1=∠2,
∴∠1=∠BCD,
∴DG∥BC.
(2)解:在Rt△BEF中,∠B=54°,
∴∠2=180°﹣90°﹣54°=36°,
∴∠BCD=∠2=36°.
又∵BC∥DE,
∴∠3=∠ACB=∠ACD+∠BCD=35°+36°=71°.
24.解:(1)设甲种产品的销售单价x元,乙种产品的销售单价y元,依题意有
![]() ,
,
解得![]() .
.
答:甲种产品的销售单价900元,乙种产品的销售单价600元;
(2)设销售甲种产品a万件,依题意有
900a+600(6﹣a)≥4400,
解得a![]() .
.
∵10000a是正整数,
∴a至少取2.6667.
答:至少销售甲种产品2.6667万件.
25.解:(1)∵(b﹣2)2+|a﹣6|![]() 0,
0,
又∵(b﹣2)2,≥0,|a﹣6|≥0,![]() 0,
0,
∴a=6,b=2,c=6.
∴M(0,6),B(2,0);
(2)①如图2﹣1中,当点P在线段OM上时,结论:∠APB+∠PBO=∠PAM;

理由:作PQ∥AM,则PQ∥AM∥ON,
∴∠1=∠PAM,∠2=∠PBO,
∴∠1+∠2=∠PAM+∠PBO,
即∠APB=∠PAM+∠PBO,
∠APB+∠PBO=∠PAM;
②如图2﹣2中所示,当点P在MO的延长线上时,结论:∠APB+∠PBO=∠PAM.
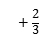
理由:∵AM∥OB,
∴∠PAM=∠3,
∵∠3=∠APB+∠PBO,
∴∠APB+∠PBO=∠PAM.
③如图2﹣3中,当点P在OM的延长线上时,结论:∠PBO=∠PAM+∠APB.
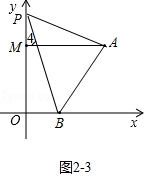
理由:∵AM∥OB,
∴∠4=∠PBO,
∵∠4=∠PAM+∠APB,
∴∠PBO=∠PAM+∠APB;
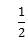
④如图4,理由:∵AM∥OB,
∴∠4=∠MAP,
∵∠PBO=∠PAB+∠4,
∴∠PBO=∠APB+∠MAP.
26.解:(1)由图②中大正方形的面积等于每个小正方形和小长方形面积之和,可得等式:
(m+n)2﹣(m﹣n)2=4mn
故答案为:(m+n)2﹣(m﹣n)2=4mn.
(2)由(1)中等式可得:
(a+b)2﹣(a﹣b)2=4ab
∵a﹣b=2,ab![]() ,
,
∴(a+b)2=(a﹣b)2+4ab=22+4![]() 9
9
故答案为:9.
(3)由题意得:![]()
整理得:![]()
①﹣②得;a=3
把a=3代入②得:b﹣3×3=0
∴b=9
∴a=3,b=9.
27.解:(1)由![]() ,
,
解得![]() .
.
(2)如图1中,作BP⊥OC于P,
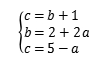
∵S△ABC+S△AOB=S四边形OABC,S四边形OABC=S△ABC+S△AOC,
∴S△AOB=S△AOC,
∴BC∥OA,
∴A(﹣a,a),
∴∠TOA=∠AON=45°,
∴∠AOT=∠BCO=45°,
∵∠CPB=90°,
∴PB=PC,
∴c=b+1,
∴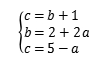 ,
,
解得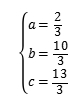 .
.
∴A(![]() ,
,![]() ),B(1,
),B(1,![]() ),
),
设直线AB的分析式为y=kx+b,则有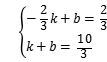 ,
,
解得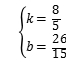 ,
,
∴直线AB的分析式为y![]() x
x![]() ,
,
∴N(0,![]() ).
).
(3)①如图2中,当点M在x轴上时,察看图象可知,点M在射线OC上,设M(m,0),过A作y轴的平行线,过B作y轴的垂线,两直线交于点F,连接FM.

∵S△MAB=S△MBC,
∴S△AFM+S△FBM﹣S△FAB=S△MBC,
∴![]() (m
(m![]() )
)![]() •|
•|![]() m|•
m|•![]() ,
,
解得m![]() 或26,
或26,
∴M(![]() ,0)或(26,0).
,0)或(26,0).
②如图3中,当点M在y轴上,且在直线BC的下方时,设M(0,n),作CF⊥OC,BF⊥CF,连接MF.
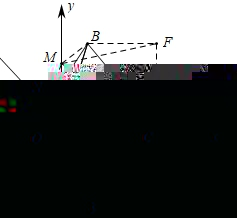
∵S△MAB=S△MBC,
∴S△MAB=S△MBF+S△MCF﹣S△BCF,
∴![]() •(
•(![]() n)•
n)•![]() (
(![]() n)
n)![]() ,
,
解得n![]() ,
,
∴M(0,![]() ).
).
③如图4中,当点M在y轴上,且在直线BC的上方时.设M(0,t).

∵S△MAB=S△MBC,
∴S△MAB=S△MOC﹣S△OBM﹣S△OBC,
∴![]() •(t
•(t![]() )•
)•![]() t
t![]() t×1
t×1![]() ,
,
解得t![]() (抛弃),
(抛弃),
综上所述,满足条件的点M的坐标为(![]() ,0)或(26,0)或(0,
,0)或(26,0)或(0,![]() ).
).






