上海八中2021学年第一学期期中考试高中一年级数学试题
1、填空题；（共12小题，每小题3分）
1.已知集合
，则
__________.
2.用列举法表示两直线
和
的交点组成的集合__________.
3.集合
，则
与
的关系是__________（用符号
或
连接）
4.命题“已知
，假如
，那样
或”是________命题.（填“真”、“假”）
5.“
”是“
”的__________条件.（用“充分非必要”、“必要非充分”、“充要”、“既非充分又非必要”填空）
6.已知
，若
是
的必要非充分条件，则实数
的取值范围是_______
7.若关于
的不等式
的解集为
，则关于的不等式
的解集为__________.
8.关于的一元二次不等式
的解集为，则的取值范围是________
9.已知，则
的范围是_________.
10.已知
，则的最大值为__________.
11.不等式对所有实数恒成立，则实数的取值范围是__________.
12.已知集合
，若集合
至多有两个子集，则的取值范围是__________.
2、选择题；（共4小题，每小题4分）
13.与
同解的不等式是（ ）
（A） （B）
（C） （D）
14.下列命题中正确的是（ ）
（A）若
，则
（B）若，则
（C）若
，则
（C）若，则
15.下列各式中，最小值为2的是（ ）
（A） （B）
（C） （D）
16.若关于的不等式有解，且解的区间长度低于5个单位长，则的取值范围是（ ）（对于区间
概念其长度为
，如区间的区间长度为2）
（A）或
（B）
或
（C）
（D）
或
3、解答卷；（共4题，本大题要有必要的过程）
17.已知
，用作差比较法证明：
18.关于的不等式组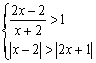
19.甲厂以千克/小时的速度匀速产某种商品（生产条件需要），每一小时所需本钱是
万元.
（1）要使生产该商品2小时所需本钱不高于30万元，求的取值范围；
（2）要使生产900千克该商品所需本钱最少，问：甲厂应该选取何种生产速度？并求最少本钱.
20.（1）当时，求关于的不等式
的解集；
（2）若不等式
的解集为
，求正实数的值.
