上海民办新竹园中学2018学年第二学期
数学学科初一阶段性诊断一试题
（完卷时间：90分钟 满分：
100分）
1、填空题（每空2分，共32分）
1.近似数5.10×
有__________个有效数字，362559精准到百位是__________
2.计算：
＝__________
3.大于﹣
小于
的整数是__________
4.已知m满足|1－m|＋
＝m，则m＝__________
5.若点N到x轴的距离为2，到y轴的距离为3，则点N的坐标为__________
6.已知a＜0，化简
－
＝__________
7.已知点P（a＋1,2a－1）关于x轴的对称点在第一象限，a的取值范围是__________
8.若a、b为实数，且b＝
＋4|a|，则a＋b的值为__________
9.两个角的两边分别平行，其中一个角比另一个角的3倍少20°。则这两个角的度数分别是
__________
10.如图所示，内错角共有__________对
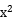A D C D A E B
1
D F C
B C A B
第10题 第11题 第12题 第13题
11.如图，将一副三角板如图所示摆设（其中一块三角板的一条直角边与另一块三角板的斜边摆设在一直线上），那样图中∠a＝__________度
12.如图，CD∥AB，∠CAD＝∠DAB，∠C＝4∠D，则∠CAB＝__________
13.如图，图形ABCD为一长条形纸带，AB∥CD，将ABCD沿EF折叠，A,D两点分别与
对应，若∠1＝∠2，则∠AEF为__________度
14.设a、b、c都是实数，且满足
，a＋bx＋c＝0，式子＋2x的算术平方根是__________
15.在平面直角坐标系XOY中，点A关于原点的对称点为（﹣1，﹣3），将点A绕（﹣2，﹣1）旋转90°后的坐标是__________
2、选择题（每题2分，共12分）
16.下列生活实例中，数学原理讲解错误的一项是（ ）
A.从一条河向一个村庄引一条最短的水渠，其中数学原理是：在同一平面内，过一点有且只有一条直线垂直于已知直线
B.两个村庄之间修一条最短的公路，其中的数学原理是：两点之间线段最短
C.把一个木条固定到墙上需要两颗钉子，其中的数学原理：两点确定一条直线
D.从一个货站向一条高速公路修一条最短的公路，其中的数学原理：联结直线外一点与直线上各点的所有线段中，垂线段最短
17.如图，下列条件：①∠1＝∠2；②∠3＝∠4；③∠B＝∠5；④∠1＋∠ACE＝180°。其中，能断定AD∥BE的条件有（ ）
A.4个 B.3个 C.2个 D.1个
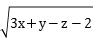
第15题 第17题 第18题
18.已知P（x，|x|），则点P肯定（ ）
A.在第一象限 B. .在第一象限或第四象限 C.在x轴上方 D.不在x轴下
19.如图，能与∠a构成同旁内角的角有
A.1个 B.2个 C.5个 D.4个
20.直线l1∥l2，D、A是l1上的任意两点，且A在D的右边，E、B是l2上任意两点，且B
在E的右边，C是l1和l2之间的某一点，联结CA和CB，则（ ）
A.∠ACB＝∠DAC＋∠CBE B.∠DAC＋∠ACB＋∠CBE＝360°
C.（A）和（B）的结论都不可能 D. （A）和（B）的结论都大概
21.如图，在△ABC中，E是BC上的一点，EC＝2BE，点D是AC的中点，设△ABC、△ADF、△BEF的面积分别为
、、，且 
－的值是（ ）
A.5 B.4 C.3 D.2
3、简答卷（第22-24题每题5分，第25-26题每题6分，共27分）
22.2
＋3
－
－
23.
－
＋
（y＜0）
24.
－2
＋－＋
＋
25.已知：
，
，求
的值
26.已知：
X、y、z合适关系式＋
＝
＋，试求x、y、z的值
4、解答卷（第27-28题每题6分，第29题8分，第30题9分，共29分）
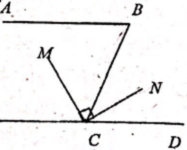
27.如图，AB∥DE，CM平分∠BCE，∠MCN＝90°，∠B＝50°，求∠DCN的度数。
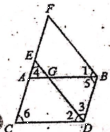
28.如图，已知∠1＝∠2，∠3＝∠4，∠5＝∠6，则ED和FB有哪些样的地方关系？请说明理由。
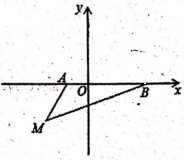
29.在平面直角坐标系中，A（a，0），B（b，0），其中a，b满足|a＋1|＋
＝0.
（1）填空：a＝__________，b＝__________；
（2）假如在第四象限内有一点M（﹣2，m），请用含m的式子表示△ABM的面积；
（3）在（2）条件下，当m＝﹣时，在y轴上有一点P，使得△BMP的面积与△ABM的面积相等，请求出点P的坐标。
30.如图1，直线MN与直线AB、CD分别交于E、F，∠1与∠2互补。
（1）填空：直线AB与直线CD的地方关系是__________
（2）如图2，∠BEF与∠EFD的角平分线交于点P，EP与CD交于点G，点H是MN上一点，且GH⊥EG，求证：PF∥GH
（3）如图3，在（2）的条件下，连接PH，K是GH上一点使∠PHK＝∠HPK，作PPQ平分∠EPK，问∠HPQ的大小是不是发生变化？若不变，请求出其值；若变化，说明理由。
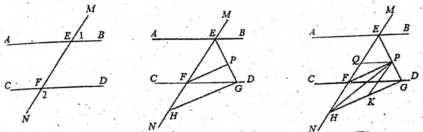
图1 图2 图3
