松江区2018学年度第一学期期末水平监控
初中三年级数学
（满分150分，完卷时间100分钟） 2019.01
考生注意：
1．本试题含三个大题，共25题．答卷时，考生务必按答卷需要在答卷纸规定的地方上作答，在草稿纸、本试题上答卷一律无效．
2．除1、二大题外，其余各题如无特不要说明，都需要在答卷纸的相应地方上写出证明或计算的主要步骤．
1、选择题：（本大题共6题，每题4分，满分24分）
【下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答卷纸的相应地方上】
1．在Rt△ABC中，∠C＝90°，假如AC＝4，BC=3，那样∠A的正切值为（ ）
（A）
； （B）
； （C）
； （D）
．
2．把抛物线
向右平移1个单位后得到的抛物线是（ ）
（A）
； （B）
； （C）
； （D）
．
3．下列各组图形肯定一样的是（ ）
（A）两个直角三角形； （B）两个等边三角形； （C）两个菱形； （D）两个矩形．
4．如图，在△ABC中，点D、E分别在边AB、AC上，假如AD=2，BD=3，那样由下列条件能判断DE∥BC的是（ ）
（A）
； （B）
； C）
； （D）
．
5．已知
为单位向量，
=
，那样下列结论中错误的是（ ）
（A）∥； （B）
； （C）与方向相同； （D）与方向相反．
6．如图，在△ABC中，D、E分别在边AB、AC上，DE∥BC，EF∥CD交AB于F，那样下列比率式中正确的是（ ）
（A）
； （B）；
（C）
； （D）
．
2、填空题：（本大题共12题，每题4分，满分48分）
【请将结果直接填入答卷纸的相应地方上】
7．已知
，那样
=_____．
8．在比率尺为1︰50000的地图上，量得甲、乙两地的距离为12厘米，则甲、乙两地的实
际距离是___________千米.
9．在Rt△ABC中，∠C＝90°，假如sinA=，BC=4，那样AB=________．
10．已知线段AB=2cm，点C在线段AB上，且AC2=BC·AB，则AC的长___________cm．
11．已知某二次函数图像的最高点是坐标原点，请写出一个符合需要的函数分析式：_______．
12．假如点、
是二次函数
（k是常数）图像上的两点，那样_______
．（填“>”、“<”或“=”）
13．小明沿坡比为1︰
的山坡向上走了100米．那样他升高了______米．
14．如图，已知直线a∥b∥c，直线m、n与a、b、c分别交于点A、C、E和B、D、F，假如AC＝3，CE＝5，DF＝4，那样BD＝_______．
15．如图，已知△ABC，D、E分别是边AB、AC上的点，且
．设
，
，那样
______________.（用向量、
表示）
16．如图，已知△ABC，D、E分别是边BA、CA延长线上的点，且DE∥BC．假如
,CE=4，那样AE的长为_______．
17．如图，已知△ABC，AB=6，AC=5，D是边AB的中点，E是边AC
上一点，∠ADE＝∠C，∠BAC的平分线分别交DE、BC于点F、G，
那样
的值为_______．
18．如图，在直角坐标平面xoy中，点A坐标为（3，2），∠AOB＝90°，∠OAB＝30°，AB与x轴交于点C，那样AC:BC的值为______．
3、解答卷：（本大题共7题，满分78分）
19．（本题满分10分）
将二次函数
的分析式化为的形式，并指出该函数图像的开口方向、顶点坐标和对称轴．
20．（本题满分10分）
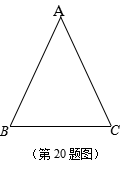
如图，已知△ABC中，AB=AC=5，cosplayA=．求底边BC的长．
21．（本题满分10分）
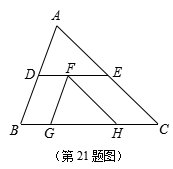
如图，在△ABC中，D、E分别是边AB、AC上的点，DE∥BC，
点F在线段DE上，过点F作FG∥AB、FH∥AC分别交BC于
点G、H，假如BG︰GH︰HC=2︰4︰3．求
的值．
22．（本题满分10分）
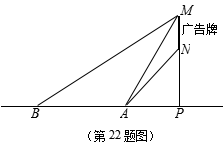某数学社团成员想借助所学的常识测量某广告牌的宽度（图中线段MN的长），直线MN垂直于地面，垂足为点P．在地面A处测得点M的仰角为58°、点N的仰角为45°，在B处测得点M的仰角为31°，AB=5米，且A、B、P三点在一直线上．请依据以上数据求广告牌的宽MN的长．
（参考数据：，
，，
，，
．）
23.（本题满分12分，第（1）小题5分，第（2）小题7分）
已知：如图，在梯形ABCD中，AD∥BC，AB=DC，E是对角线AC上一点，且AC·CE=AD·BC.
（1）求证：∠DCA=∠EBC；
（2）延长BE交AD于F，求证：AB2=AF·AD.
24.（本题满分12分，第（1）小题3分，第（2）小题4分，第（3）小题5分）
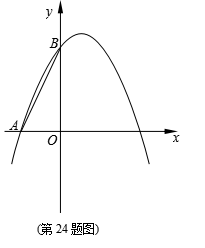
如图，抛物线
经过点A（﹣2，0），点B（0，4）.
（1）求这条抛物线的表达式；
（2）P是抛物线对称轴上的点，联结AB、PB，假如∠PBO=∠BAO，求点P的坐标；
（3）将抛物线沿y轴向下平移m个单位，所得新抛物线与y轴交于点D，过点D作DE∥x轴交新抛物线于点E，射线EO交新抛物线于点F，假如EO=2OF，求m的值.
25．（本题满分14分，第（1）小题4分，第（2）、（3）小题各5分）
如图，已知△ABC中，∠ACB=90°，D是边AB的中点，P是边AC上一动点，BP与CD相交于点E．
（1）假如BC=6，AC=8，且P为AC的中点，求线段BE的长；
（2）联结PD，假如PD⊥AB，且CE=2，ED=3，求cosplayA的值；
（3）联结PD，假如，且CE=2，ED=3，求线段PD的长．
