第一章:数的整除
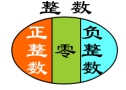
1. 零和正整数统称为自然数。正整数、零、负整数统称为整数。
重点题型：
1. 在8，－10，0，0.25，－50，
，100，－8.5中，正整数有__________，
自然数有__________，整数有__________
2.最小的自然数是__________
提升：非负整数，如小于3的非负整数有__________
2. 整数a除以整数b，假如除得的商是整数而余数为零，大家就说a能被b整除，或者说b能整除a。
用式子表示:假如 a÷b=c称a能被b整除或b能整除a。（区别两种表述）
重点题型：
1. 下列各组数中，第一个数能被第二个数整除的是__________，第二个数能整除第一个数的是__________
12和24；39和13；54和27；46和4；17和51；84和7
2. 12÷3=4，那样__________能被__________整除；__________能整除__________
3. 整除的条件:
1）除数，被除数都为整数
2）被除数除以除数，商是整数而且余数为零。
重点题型：
小明觉得2.5能被5整除。这种说法对吗？
4. 整数a被整数b整除,a叫b的倍数,b叫a的因数
因数和倍数是相互依存的。
要紧结论：
一个整数的因数的个数是__________ 的，其中最小的因数是__________ ，最大的因数是__________ 。
一个整数的倍数的个数是__________ 的，其中最小的倍数是__________，
一个整数__________最大的倍数。
重点题型：
1. 由于4÷2=2,所以4是倍数,2是因数，这种说法对吗？
2. 一个整数的最大因数减去这个正整数的最小倍数，所得的差肯定（ ）
A <0 B =0 C >0 D 不等于0
3. 会求一个数的因数：如求105的因数
4. 会求一个数的倍数：如求7的倍数（写出5个）
5. 任何一个正整数至少有两个因数。
6. 假如一个数既是12的因数,又是12的倍数,那样这个数肯定是__________。
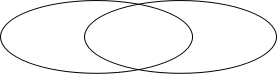7. 18的因数 24的因数
18和24的最大公因数是__________
5. 能被2整除的数的特点：个位上的数是0，2，4，6，8
能被5整除的数的特点：个位上的数是0，5
能被10整除（既能被2整除又能被5整除）的数的特点：个位上的数是0
能被3整除的数的特点：各位上的数字的和能被3整除
能被9整除的数的特点：各位上的数字的和能被9整除
重点题型：
1. 在15,27,38,62,90,135,420这七个数中:
1)能被2整除的数是__________。2)能被5整除的数是__________。
3)既能被2整除,又能被5整除的数是__________。
4)能被3整除的数是__________。5)能被9整除的数是__________。
6. 能被2整除的整数叫做偶数,不可以被2整除的整数叫奇数
奇数 1,3,5,7,9,11,13,……… 偶数 2,4,6,8,10,12,14,………
重点题型：
1. 假如连续三个偶数之和是42，那样这三个数是（ ）
2. 三个连续的偶数中,最大的是a，最小的是
7. 奇数＋奇数＝偶数 偶数＋偶数＝偶数 奇数＋偶数＝奇数
奇数－奇数＝偶数 偶数－偶数＝偶数 奇数－偶数＝奇数
奇数×奇数＝奇数 偶数×偶数＝偶数 奇数×偶数＝偶数
8. 一个正整数,假如只有1和它本身两个因数,如此的数叫做素数,也叫质数；
假如除去1和它本身以外还有别的因数,如此的数叫合数，合数总可以写成几个素数相乘的形式
1不是素数更不是合数
正整数
素数 1 合数
100以内的素数
2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 |
29 | 31 | 37 | 41 | 43 | 47 | 53 | 59 | 61 |
67 | 71 | 73 | 79 | 83 | 89 | 97 |
|
|
熟记20以内的全部素数
重点题型：
1. 把下列各数填入适合的圈内。
11，21，87，31，97，57，33，41，51，61,71，39，81，69，91
素数 合数
2. 最小的奇数又是素数的是__________，10以内最大的偶数又是合数的是__________
最小的合数是__________最小的奇数又是合数的是__________
9. 每一个合数都可以写成几个素数相乘的形式,其中每一个素数都是这个合数的因数,叫做这个合数的素因数。把一个合数用素因数相乘的形式表示出来,叫做分解素因数。
重点题型：
1. 105分解素因数为__________，105的素因数有__________，因数有__________
36分解素因数为__________，36的素因数有__________，因数有__________
第10点为¶第一章最重点的内容
10. 几个数公有些因数，叫做这几个数的公因数；其中最大的一个叫做最大公因数。
几个整数公有些因数，叫做这几个数的公因数；其中最大的一个叫做最大公因数。
求几个整数的最大公因数，只须把它们所有公有些素因数连乘，所得的积就是它们的最大公因数
求两个整数的最小公倍数,只须取它们所有公有些素因数,再取它们各自剩余的素因数,将这类数连乘,所得的积就是这两个数的最小公倍数
两个整数中，假如某个数是另一个数的因数，那样这个数就是这两个数的最大公因数；假如这两个数互素，那样它们的最大公因数是1。
两个整数中，假如某个数是另一个数的倍数，那样这个数就是这两个数的最小公倍数；假如这两个数互素，那样它们的最小公倍数是它们的乘积。
两个整数只有公因数1，那样称这两个数互素。
与和最大公因数及最小公倍数有关的应用问题
如：（不必抄题，仅需写出解答过程）
重阳节,欣欣中学的师生到敬老院看望老人,他们共筹备了320个苹果,240个橘子,200个梨,来慰问老人。问用这类果品,最多可以分成多少份同样的礼物？在每份礼物中,苹果、橘子、梨各多少个？
某车站,每隔8分钟开出一辆电车,每隔10分钟开出一辆汽车。上午9时,有一辆电车与一辆汽车同时开出,求9时将来再过多长时间电车与汽车首次同时发车？
重点题型：
1. 求30和42的最大公因数和最小公倍数
2. 求30、42和21的最大公因数和最小公倍数
3. 一筐苹果,2个一拿,3个一拿,4个一拿,5个一拿都正好拿完而没余数,这筐苹果最少应
有
120个 90个
60个 30个
4. （重点）已知甲数＝2×3×5×7，乙数＝2×2×5×5×7，、
甲数和乙数的最小公倍数是__________最大公因数是__________
5. （重点）在2，5，8，15中，共有__________对互素，它们是__________
第二章：分数
1. 两个正整数相除,它们的商可用分数表示。被除数÷除数= 
用字母表示: p÷q = 
整数看成是特殊的分数,即分母为1的分数。
重点题型：
1. 用分数表示下列除法的商:如7÷8＝____________________
2. 把下列分数写成两个数相除的式子: 
＝__________÷__________
3. （重点）把一根2米长的绳子剪成长度相等的5段,那样每段绳子长多少米？每段是
这根绳子的几分之几？
4. 一项工程甲队独做10天完成,那样平均天天完成这项工程的__________
5. 把5个同样大小的苹果平均分给3个小朋友,那样每一个小朋友分得__________个
6. （重点）修路队7天修完一条长2千米的公路，那样平均天天修__________千米，平均天天修了这条公路的__________
2. 数轴问题：（主要两类问题必会）
1）用数轴上的点表示分数
2）写出数轴上点所表示的分数
重点题型：
1. 在数轴上表示分数
，
，
3. 分数的基本性质
分数的分子和分母都乘以或都除以同一个不为零的数,所得的分数与原分数的大小相等。
即
重点题型：
1. 
2. 写出三个与下列各数分母不同而大小相等的分数
3. 把 和 分别化成分母是15且与原分数大小相等的分数。
4. （重点定义）分子和分母互素的分数数叫最简分数。分子和分母互素,大家把如此的分数叫最简分数
求一个数是另一个数的几分之几用除法，如a是b的几分子几，写成a÷b（及有关应用题）
重点题型：
1. 指出以下什么分数是最简分数,把不是最简分数的分数化为最简分数:
,
,,
,,
,
,
。（常出目前选择题中，必会）
2. 15分钟是1小时的几分之几？（单位必须要统一后再做）
3. 一个分数它的分母是56,化成最简分数是 ,这个分子原来是， 这个分数原来是
4. 假如甲数除以乙数是
,那样乙数是甲数的
5. 有关应用题（统计图、统计表）必会（应用题不必抄题）
小学六年级某班在一次数学测验中的成绩如下，试依据表中的数据解答下列问题：
成绩（分） | 60分以下 | 60～69 | 70～79 | 80～89 | 90～100 |
人数 | 2 | 6 | 12 | 14 | 11 |
（1）成绩不合格（60分以下）的学生人数占全班总人数的几分之几？
（2）成绩优良（80分及以上）的学生人数占全班总人数的几分之几？
6. 在100以内（含100）的正整数中，素数有25个，素数的个数占这100个数的__________，素数的个数是合数的个数的__________
4. 将异分母的分数分别化成与原分数大小相等的通分母的分数,这个过程叫做通分。通分的依据是什么分数的基本性质
重点题型：
1. （必会，并注意正确格式）把下列每组中的各分数通分，并比较大小
和 
、和（假如没限制必须要用通分的办法，还可以使用拆项的办法，请用两种办法完成）
2. 写出两个比
小，比大的最简分数，介于两个数之间的最简分数有多少个？
友情提示：看清题目中是从小到大排列还是从大到小排列
小学六年级第二学期数学常识大全
第五章 有理数
第一节 有理数
5.1 有理数的意义
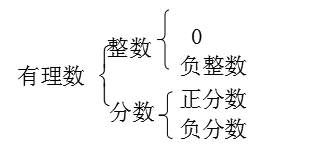
零不是正数更不是负数。
假如把整数看成分母为1的分数，那样在这个意义下，所有些有理数都是分数。
想一想：什么数是非负数、非正数？
练一练：
1. 下列说法正解的是（ ）
A．非负有理数就是正有理数。 B. 零表示没有，无实质意义。
C．正整数和负整数统称为整数。 D. 整数和分数统称为有理数。
2．把下列和数填入相应的大括号内：
－7，3.01，300%，-0.142857，+0.1，0，
，
（1）整数集：{ …}
（2）分数集：{ …}
（3）正整数集：{ …}
（4）负分数集：{ …}
3．下列说法对不对？为何？
（1）一个有理数，不是整数就是分数；
（2）一个有理数，不是正数就是负数。
5.2 数轴
三要点：原点、正方向、单位长度
你能画一条数轴吗？
概念：相反数
只有符号不一样的两个数，大家称其中一个数为另一个数的相反数，也称这两个数互为相反数，零的相反数是零。
5.3 绝对值
概念：表示一个数到原点的距离（非负数）
想一想：数a的绝对值等于什么？
a-b的绝对值又等于什么？
第二节 有理数的运算
5.4 有理数的加法
加法法则：一般地，同号两数相加，取与加数相同的符号，并把绝对值相加；
异号两数相加，取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值；
互为相反数的两个数相加得零； 一个数同零相加，仍得这个数；
有理数加法运算的步骤：先确定结果的符号，再计算结果的绝对值。
加法方法：相反数的先抵消，同分母的放一块，正与正，负与负，同号相加，异号相减
加法的交换律：两个有理数相加，交换加数的地方，和不变，即
；
加法的结合律：三个有理数相加，先把前两个数相加，或者先把后两个数相加，和不变，
即
；
5.5 有理数的减法
1、减去一个数等于加上这个数的相反数
2、0减去一个数等于这个数的相反数
5.6 有理数的乘法
有理数乘法法则：两数相乘，同号得正，异号得负，并把绝对值相乘；任何数与零相乘，积为零。
乘方方法：带分化假分，乘法化除法，统一约分再计算
渗透化归思想，有理数的乘法事实上就是在确定完积的符号后，转化为小学中算术数的乘法。
练一练：
一个数与它的相反数的积__________。
一个数与__________的积是它本身；一个数与__________的积是它的相反数。
三个有理数的积为0,那样，这三个数中至少__________；三个数的积是负数，那样，这三个数的符号状况是__________。
－2的倒数是__________；0.1的倒数是__________；－3的倒数是__________；12的倒数是__________；－22的倒数是__________。
假如两个数的积是－1,大家称它们互为负倒数。那样，－2的负倒数是__________；0.01的负倒数是__________。
一个数的倒数是它本身，这个数是__________。
用“＞”或“＜”号连接：假如 a＜0，b＜0，那样 ab__________0；假如 a＜0，b＜0，那样ab __________0；假如a＞0时，那样a __________2a；假如a＜0时，那样a __________2a．
5.7 有理数的除法
1、同号得正，异号得负
2、绝对值相除
3、除化乘
4、0除以一个数等于0
练一练：
（1）（＋15）×31÷（－15）； （2）－6÷（－0.25）×24；
5.8 有理数的乘方
底下的数叫底数，指头指的数叫指数，乘方的结果叫幂。
5.9 有理数的混合运算（计算规则）
先乘方，再乘除，后加减；
同级运算左到右；
一块通分再计算；
含有括号小到大；
去括号时要小心；
要小心啊要小心；
负号后面睁大眼；
去掉括号变符号。
5.10 科学记数法
×10n（1≤＜10， n=整数位数-1）
e.g.: 200000000=2×108
第六章 一次方程（组）和一次不等式（组）
第一节 方程与方程的解
6.1 列方程
一个长方形篮球场的周长为86米，长是宽的2倍少2米，这个篮球场的长与宽分别是多少米？
用两种办法列式：
方程：设这个篮球场的宽为
米，则长为（2-2）米
2（2-2+）=86
想一想：你能再列一种方程吗？你还可以用列式计算吗？
6.2 方程的解
判断一个数是不是是方程的解（2+3=9）（=3）
办法：
检验：将=3代入原方程
左侧=2×3+3=9
右侧=9
∵左侧=右侧
∴=3是原方程的解
第二节 一元一次方程
6.3 一元一次方程及其解法
Part1
等式的性质：1、等式两边同时加上（或减去）同一个数或同一个含有字母的式子，所
得结果仍是等式。
2、等式两边同时乘以（或除以）同一个不为0的数，所得结果仍是等
式。
Part2
4-=2+4
解：4-3-1=2+4 去括号
4-2=4+3+1 移项 缺一不可
2=8 化
（≠0）格式（一元一次方程的一般形式）
=8 化
格式 （将系数化为1）
Part3
解方程过程：
去分母
去括号
移项
化（≠0）格式
化格式
6.4 一元一次方程的应用
一个长方形篮球场的周长为86米，长是宽的2倍少2米，这个篮球场的长与宽分别是多少米？
解：设这个篮球场的宽为米，则长为（2-2）米
2（2-2+）=86
4-4+2=86
6=90
=15
2-2=28
答：这个篮球场的长为28米，宽为15米。
第三节 一元一次不等式（组）
6.5 不等式及其性质
1、用＞，＜，≥，≤，≠表示的关系式叫做不等式
2、不等式的性质1：不等式两边加（或减）同一个数（或式子），不等号的方向不变。
3、不等式的性质2：不等式两边乘（或除以）同一个正数，不等号的方向不变。
4、不等式的性质3：不等式两边乘（或除以）同一个负数，不等号的方向改变。
6.6 一元一次不等式的解法
1、不等式的解：在含有未知数的不等式中，能使不等式成立的未知数的值叫不等式的解。
不等式的解有无数个。
1、解不等式：2-5≥8（4+5）
解：2-5≥8（4+5） 去分母
2-5≥32+40 去括号
2-32≥40+5 移项
-30≥45 合并
≤-1.5 系数化为1
6.7一元一次不等式组
同大取大，同小取小；
大于小的，小于大的，取中间；
大于大的，小于小的，无解。
数轴画图求解法
第四节 一次方程组
6.8 二元一次方程
1、含有两个未知数的一次方程叫做二元一次方程
2、使二元一次方程两边的值相等的两个未知数的值，叫做二元一次方程的解。（有无数个解）
6.9 二元一次方程组及其解法
1、由几个方程组成的一组方程叫做方程组。假如方程组中含有两个未知数，而且未知数的项
的次数都是一次，那样如此的方程组叫做二元一次方程组。
2、在二元一次方程组中，使每一个方程都合适的解，叫做二元一次方程组的解。
3、通过“代入”消去另一个未知数，将方程组转化为一元一次方程，这种解法叫做代入消元
法，简称代入法。
4、通过将两个方程相加（或相减）消去一个未知数，将方程组转化为一元一次方程，这种解
法叫做加减消元法
6.10三元一次方程组及其解法
1、假如方程组中含有三个未知数，且含有未知数的项的次数都是一次，如此的方程组叫做三
元一次方程组。
2、三元一次方程组——消元——二元一次方程组——消元——一元一次方程组
6.11 一次方程组的应用
e.g.:班委会花100元购买了笔记本和钢笔共22件作为班级奖品，假如每本笔记本的价格是2.5
元，每支钢笔的价格是7元，那样班委会购买了多少本笔记本、多少支钢笔？
解：设买了个笔记本，
支钢笔，
+=22 ①
2.5+7=100 ②
由①得：=22-③
由③代入二得：=12④
由④代入①得：=10
答：买了12个笔记本，10支钢笔。
第七章 线段与角的画法
第一节 线段的相等与和、差、倍
7.1 线段的大小的比较
1、 直线
线段
射线
2、比较大小技巧：
①用尺量
②目测
③圆规
④叠合法
两点之间，线段最短。
两点间的距离：联结两点的线段的长度。
用尺规作出一条线段，使
①作射线
②在射线上，截取线段
所以线段AB即为所求
7.2 画线段的和、差、倍
1、画图
和：画线段
所以线段即为所求
差：画线段
所以线段即为所求
倍（线段中点）：画线段的中点
所以点B即为所求
第二节 角
7.3 角的定义与表示
1、角：①具备公共端点的两条射线组成的图形
边
顶点 边
②由一条射线绕着它的端点旋转到另一个地方所成的图形
终边
2、①外部 内部
始边
② 外部
内部
3、①平角：180°
②周角： 360°
③直角：
90°
4、角的表示办法：①大写字母：∠
（或∠）
②当角唯一时用顶点表示：∠
③希腊字母表示：∠
，∠
，∠
……
④数字表示：∠1，∠2……
5、方向角：
50°
表示为南偏西50°
7.4 角的大小的比较
1、画一个角，使它等于已知角
E A H D
O α B M C
F G
①画射线MC
②以O为圆心，任意长为半径画弧交OA，OB于点E，F
③以M为圆心，OE为半径画弧，交MC于点G
④以G为圆心，OF为半径画弧，交前弧于点H
⑤作射线MH
所以∠HMC即为所求
7.5 画角的和、差、倍
1、三角尺和、差、倍：
①两角和：75°，120°，105°，150°，180°、
②两角差：15°，30°45°60°
③三角和：……
都是15°的倍数
2、画∠α-∠β=∠γ
α β
γ
α
β
3、平分线：H
A
C E
O D B
7.6 余角、补角
1、若∠1+∠2=90°，则∠1是∠2的余角（或∠2是∠1的余角）
∠1与∠2互为余角，简称互余
2、若∠1+∠2=180°，则∠1是∠2的补角（或∠2是∠1的补角）
∠1与∠2互为补角，简称互补
3、若∠1与∠2的互余，则∠1+∠2=90°
若∠1与∠2的互补，则∠1+∠2=180°
4、性质：同（等）角的余角相等
同（等）角的补角相等
5、1°=60′（你知不知道？）
1′=60″
第八章 长方体的再认识
第一节 长方体的元素
1、长方体的元素：6个面，12条楞，8个顶点。
2、每一个面都是长方形。
3、4条长、宽、高。
4、对面相同
5、公式：
h
a b
S表=2S1+2S2+2S3
V=a·b·h
=S底·h
想一想：
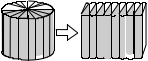把一个底面半径6厘米、高8厘米的圆柱体，切拼成一个近似的长方体，
表面积比原来增加了（ ）平方厘米。
练一练：
一个长方体的棱长之和为48厘米，长5厘米，宽4厘米，高（ ）厘米。
第二节 长方体的直观图的画法
1、平面：平的面，无边沿
2、斜二测画法：
画长5cm，宽3cm，高4cm的长方体
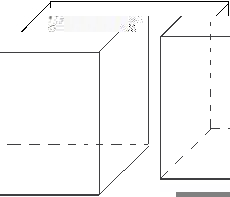
所以长方体ABCD-EFGH即为所求
第三节 长方体中棱与棱地方关系的认识
1、 平行 相交
2、在__________两条楞的地方关系
相交 斜交
平行 垂直
异面
3、在__________两条楞的地方关系 （异面）
4、长方体中与一条楞平行的楞有3条
垂直的楞有4条
异面的楞有4条
第四节 长方体中棱与平面地方关系的认识
1、棱与平面地方关系
①平面上 ②相交 斜交 ③平行
垂直
2、长方体中与一条楞平行的平面有2个
垂直的平面有2个
长方体中与一个面平行的楞有4条
垂直的楞有4条
3、怎么样检验棱与平面垂直：
①三角尺法
②铅垂线法
③合页型折纸法
4、怎么样检验棱与平面平行：
①铅垂线法
②长方形纸片法
第五节 长方体中平面与平面地方关系的认识
1、平面α⊥平面β 平面α∥平面β
平面β 平面α
平面α
平面β
2、怎么样检验平面与平面垂直：
①铅垂线法（当为水平面时）
②合页型折纸法
③三角尺法
3、怎么样检验平面与平面平行：
①铅垂线法（当为水平面时）
②长方形纸片法（放两次）
