上海奉贤中学高中二年级上学期数学期中考试
(考试时间120分钟 满分150分)命题:陆玉兰、金小峰 审题:姚建新
1、填空题(第1-6题每小题4分,第7-12题每小题5分)
1.已知直线![]() 过点
过点![]() ,且其法向量
,且其法向量![]() ,则直线
,则直线![]() 的点方向式方程为__________
的点方向式方程为__________
2.若关于![]() 的二元一次线性方程组的增广矩阵为
的二元一次线性方程组的增广矩阵为![]() ,且该方程组的解为
,且该方程组的解为![]() ,则
,则![]() 的值为__________
的值为__________
3.方程组![]() 有无穷多组解,则实数
有无穷多组解,则实数![]() ___________
___________
4.已知对于任意的![]() ,直线
,直线![]() 都经过一个定点,则该定点的坐标为___________
都经过一个定点,则该定点的坐标为___________
5.已知向量![]() 与
与![]() 的夹角为
的夹角为![]() ,
,![]() ,则
,则![]() __________
__________
6.已知![]() ,则
,则![]() 在
在![]() 上的投影等于______________
上的投影等于______________
7.已知点![]() ,若直线
,若直线![]() 过点
过点![]() ,且与线段
,且与线段![]() 相交,则该直线
相交,则该直线![]() 的斜率的取值范围是___________
的斜率的取值范围是___________
8.三阶行列式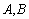
![]() 中元素
中元素![]() 的代数余子式的值记为
的代数余子式的值记为![]() ,则
,则![]() ________________
________________
9.![]() 中,
中,![]() ,
,![]() 是边
是边![]() 上一点,若
上一点,若![]() ,则点
,则点![]() 的坐标是_______________
的坐标是_______________
10.设实数![]() 满足
满足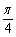 ,若
,若![]() 的最大值为12,则
的最大值为12,则![]() 的取值范围是___________________
的取值范围是___________________
11.已知![]() 为
为![]() 的外心,若
的外心,若![]() ,则
,则![]() 的最大值为___________
的最大值为___________
12.设单位向量![]() 的夹角为锐角,若对于任意
的夹角为锐角,若对于任意![]() ,都有
,都有![]() 成立,则
成立,则![]() 的最小值为______________
的最小值为______________
2、选择题(每小题5分)
13.![]() 是两个非零向量,若函数
是两个非零向量,若函数![]() 的图像是一条直线,则必有( )
的图像是一条直线,则必有( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
14.在![]() 中,
中,![]() 分别是内角
分别是内角![]() 所对的边,若
所对的边,若![]() (其中
(其中![]() 表示
表示![]() 的面积),且
的面积),且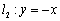 ,则
,则![]() 的形状是( )
的形状是( )
A.有一个角为30°的等腰三角形 B.等边三角形
C.直角三角形 D.等腰直角三角形
15.已知![]() 中,
中,![]() 分别是内角
分别是内角![]() 所对的边,
所对的边,![]() 为边
为边![]() 上的高,有以下结论:①
上的高,有以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,则其中正确的结论个数为( )
,则其中正确的结论个数为( )
A.1个 B.2个 C.3个 D.4个
16.已知两个不相等的非零向量![]() ,两组向量
,两组向量![]() 和
和![]() 均由2个
均由2个![]() 和3个
和3个![]() 排列而成。记
排列而成。记![]() ,则
,则![]() 表示
表示![]() 所大概取值中的最小值,有以下结论:①
所大概取值中的最小值,有以下结论:①![]() 有5个不一样的值;②若
有5个不一样的值;②若![]() ,则
,则![]() 与
与![]() 无关;③若
无关;③若![]() ,则
,则![]() 与
与![]() 无关;④若
无关;④若![]() ,则
,则![]() ;⑤若
;⑤若![]() ,则
,则![]() 与
与![]() 的夹角为
的夹角为![]() ,则正确的结论的序号的是( )
,则正确的结论的序号的是( )
A.①②④ B.②④ C.②③ D.①⑤
3、解答卷(14分+14分+14分+16分+18分)
17.已知两点![]()
(1)求直线![]() 的方程;
的方程;
(2)已知实数![]() ,求直线
,求直线![]() 的倾斜角
的倾斜角![]() 的取值范围.
的取值范围.
18.已知在平行四边形![]() 中,
中,![]() ,边
,边![]() 的长分别为2,1,若
的长分别为2,1,若![]() 分别是
分别是![]() 上的点,
上的点,
(1)若![]() 分别是
分别是![]() 上的中点,求
上的中点,求![]() 的值。
的值。
(2)若点![]() 满足
满足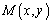 ,求
,求![]() 的取值范围。
的取值范围。
19.已知![]() ,若过定点
,若过定点![]() 且以
且以![]() 为法向量的直线
为法向量的直线![]() 与过定点
与过定点![]() 且以
且以![]() 为法向量的直线
为法向量的直线![]() 相交于动点
相交于动点![]() 。
。
(1)求直线![]() 和
和![]() 的方程。
的方程。
(2)若直线![]() 的斜率为
的斜率为![]() 、直线
、直线![]() 的斜率为
的斜率为![]() ,求
,求![]() 的值,并求点
的值,并求点![]() 的轨迹方程。
的轨迹方程。
20.如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与直线
与直线![]() 之间的阴影部分记为
之间的阴影部分记为![]() ,地区
,地区![]() 中动点
中动点![]() 到
到![]() 的距离之积为1.
的距离之积为1.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)对于地区![]() 中动点
中动点![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)动直线![]() 穿过地区
穿过地区![]() ,分别交直线
,分别交直线![]() 于
于![]() 两点,若直线
两点,若直线![]() 与点
与点![]() 的轨迹
的轨迹![]() 有且只有一个公共点,求证:
有且只有一个公共点,求证:![]() 的面积值为定值.
的面积值为定值.

21.出租车几何学是由十九世纪的赫尔曼·闵可夫斯基所创立的。在出租车几何学中,点还是形如![]() 的有序实数对,直线还是满足
的有序实数对,直线还是满足![]() 的所有
的所有![]() 组成的图形,角度大小的概念也和原来一样,直角坐标系内任意两点
组成的图形,角度大小的概念也和原来一样,直角坐标系内任意两点![]() 概念它们之间的一种“距离”:
概念它们之间的一种“距离”:![]() ,请解决以下问题:
,请解决以下问题:
(1)求线段![]() 上一点
上一点![]() 到点
到点![]() 的“距离”;
的“距离”;
(2)概念:“圆”是所有到定点“距离”为定值的点组成的图形,求“圆”上的所有点到点![]() 的“距离”均为
的“距离”均为![]() 的“圆”方程,并求该“圆”围成的图形的面积;
的“圆”方程,并求该“圆”围成的图形的面积;
(3)若点![]() 到点
到点![]() 的“距离”和点
的“距离”和点![]() 到点
到点![]() 的“距离”相等,其中实数
的“距离”相等,其中实数![]() 满足
满足![]() ,求所有满足条件的点
,求所有满足条件的点![]() 的轨迹的长之和。
的轨迹的长之和。






