桃浦中学2018-2019学年第学期期末考试
高二数学试题
(考试时间:
100 分钟 满分: 100分)
1、填空题:(本大题满分36分,每题3分)
1、已知集合![]() ,若
,若![]() , 则
, 则![]() _________.
_________.
答案:3
2、函数![]() 的概念域为_________.
的概念域为_________.
答案:[-1,1]
3、满足不等式![]() 的
的![]() 的取值范围是_________.
的取值范围是_________.
答案:
4、若幂函数![]() 的图像经过点
的图像经过点![]() ,则此幂函数的分析式是_________.
,则此幂函数的分析式是_________.
5、若点![]() 在函数
在函数![]() 图像上,则
图像上,则![]() 的反函数为_________.
的反函数为_________.
6、函数![]() 的零点是._________
的零点是._________
7、方程![]() 的解
的解![]() _________.
_________.
8、设函数![]() ,则
,则![]() _________.
_________.
9、设![]() ,若函数
,若函数![]() 是偶函数,则
是偶函数,则![]() 的单调递增区间是_________.
的单调递增区间是_________.
10、关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,则实数
,则实数![]() 的取值范围是_________.
的取值范围是_________.
11、若函数![]() 是奇函数,则实数
是奇函数,则实数![]() 的值是_________.
的值是_________.
12、已知![]() ,集合
,集合![]() ,记
,记![]() , 则
, 则![]() _________.
_________.
2、选择题:(本大题满分16分)
13、若![]() 则下列不等关系中,不可以成立的是( ) .
则下列不等关系中,不可以成立的是( ) .
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
14、下列命题:(1)偶函数的图像-定![]() 轴相交;(2)奇函数的图像肯定通过原点;(3)既是奇函数又是偶函数的函数肯定是
轴相交;(2)奇函数的图像肯定通过原点;(3)既是奇函数又是偶函数的函数肯定是![]() ,(4)函数的图像关于原点中心对称是这个函数为奇函数的充要条件,其中正确的命题个数是( )
,(4)函数的图像关于原点中心对称是这个函数为奇函数的充要条件,其中正确的命题个数是( )
A、1 B、2 C、3 D、4
15、 设奇函数![]() 在区间
在区间![]() 上是增函数,且其最小值是4,则
上是增函数,且其最小值是4,则![]() 在区间
在区间![]() 上是( )
上是( )
A、增函数且最小值为-4 B、增函数且最大值为-4
C、减函数且最小值为-4. D、减函数且最大值为-4
16、已知函数![]() 的反函数为
的反函数为![]() ,则函数
,则函数![]() 与
与![]() 的图像( )
的图像( )
A、关于![]() 轴对称 B、关于原点对称
轴对称 B、关于原点对称
C、关于直线![]() 对称 D、关于直线
对称 D、关于直线![]() 对称
对称
3、简答卷:(本大题满分48分)
17. (本题满分8分)
已知不等式![]() 的解集为
的解集为![]() ,函数
,函数![]() 的概念域为集合
的概念域为集合![]() ,求
,求![]() .
.
18. (本题满分8分)
已知函数![]() 。若
。若![]() ,求
,求![]() 的最大值和最小值.
的最大值和最小值.
19. (本题满分10分)
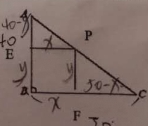
如图,某校有一块形如直角三角形![]() 的空地,其中
的空地,其中![]() 为直角,
为直角,![]() 长40米,
长40米,![]() 长50米现欲在此空地上建造一间健身俱乐部,其占地形状为矩形
长50米现欲在此空地上建造一间健身俱乐部,其占地形状为矩形![]() ,且
,且![]() 为矩形的一个顶点,求该健身俱乐部的最大占地面积.
为矩形的一个顶点,求该健身俱乐部的最大占地面积.
20.(本题满分10分,第1小题4分,第2小题6分)
设函数![]() .
.
(1)求函数![]() 的值城和零点;
的值城和零点;
(2)请判断函数![]() 的奇偶性和单调性,井给予证明,
的奇偶性和单调性,井给予证明,
21 (本题满分12分,第1小题6分,第2小题6分)
已知函数![]() 的反函数为
的反函数为![]() .记
.记![]() )
)
(1)求函数![]() 的最小值;
的最小值;
(2)集合![]() 对于任意的
对于任意的![]() ,
,
不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围。
的取值范围。







