初三数学暑期集训基础训练（15）
阶段复习测试3
1. 下列方程为一元二次方程的是
A．ax2+bx+c=0 B．x2－2x－3 C．2x2＝0 D．xy＋1＝0
2. 关于
的一元二次方程（a-1）x2+x+a2-1=0的一个根是0，则
值为（ ）
A、
B、
C、或 D、0
3. 关于x的一元二次方程（a+1）x2－4x－1=0有两个不相等的实数根，则a的取值范围是 （ ）
A．a＞－5 B．a＞－5且a≠－1 C．a＜－5 D．a≥－5且a≠－1
4. 已知点P是线段OA的中点，P在半径为r的⊙O外，点A与点O的距离为8，则r的取值范围是（）
A．r ＞4 B．r＞8 C．r ＜4 D．r ＜8
5. 下列方程中两根之和为2的方程个数有： （ ）
A． 1 B．2 C． 3 D．4
6. 如图，OA，OB是⊙O的半径，点C在⊙O上，连接AC，BC，若∠A=20°,∠B=70°，
则∠ACB的度数为 （ ）
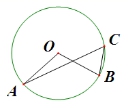A．50° B．55° C．60° D．65°
第5题图 第10题图
7.以下命题：①直径相等的圆是等圆； ②长度相等弧是等弧； ③相等的弦所对的弧也
相等； ④圆的对称轴是直径⑤相等的圆周角所对的弧相等；其中正确的个数是（ ）
A．4 B．3 C．2 D．1
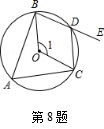
8. 如图所示，已知四边形ABDC是圆内接四边形，∠1=112°，则∠CDE=（ ）
A．56° B．68° C．66° D．58°
9. 若圆的一条弦把圆分成度数的比为1：3的两条弧，则弦所对的圆周角等于（ ）
A. 45° B. 90° C. 135° D. 45° 或135°
10. 如图是由三个边长分别为6、9、的正方形所组成的图形，若直线AB将它分成面积相等的两部分，则的值是（ ）
A.1或9 B.3或5 C.4或6 D.3或6
11. 一元二次方程（x-2）=x+1化为一般形式是__________.
12. 写一个二次项系数为1的一元二次方程，使得两根分别是-2和1. _______________
13. 如图，AD为⊙O的直径，∠ABC＝75º，且AC＝BC，则∠BDE＝__________.
14. 已知m，n是方程x2－2x－5=0的两个实数根，则m2+2n的值为_______
15. 已知
，
（a为任意实数），则M、N的大小关系为________
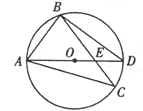
第13题图
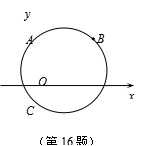
16. 如图，在直角坐标系中，点A、B、C的坐标分别为（0，3）、（4，3）、（0，－1），则△ABC外接圆的圆心坐标为__________．
17. 若小唐同学掷出的铅球在场地上砸出一个直径约为8cm、深约为2cm的小坑，则该铅球的直径约为__________cm
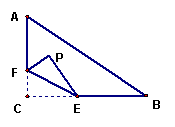
18. 如图，在RtΔABC中，∠C＝90°，∠A＝60°AC＝6，，点F在边AC上，并且CF＝2，点E为边BC上的动点，将ΔCEF沿直线EF翻折，点C落在点P处，则点P到边AB距离的最小值是____________________.
19.解方程：
（1）22-8=0 （2 ）2x2−
x-1=0 x2-3x+1=0
（4）（x+3)＝5. （x-1）2-5（x-1）+6=0
20. 在等腰△ABC中，三边分别为a、b、c，其中a=5，若关于x的方程x2+x+6-b=0有两个相等的实数根，求△ABC的周长．
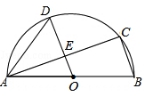
21. 如图，在平行四边形ABCD中，E是AD上一点，延长CE到点F，使∠FBC=∠DCE
求证∠D=∠F
用直尺和圆规在AD上作出一点P，使∠BPC=∠D（保留作图痕迹，不写作法）。
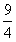
22.关于x的方程
有两个不相等的实数根（1）求k的取值范围（2）是不是存在实数k，使得方程的两个实数根的倒数和等于0？若存在求出K的值，若没有，说明理由。
23. 为进一步进步教育事业，自2016年以来，淮安加强了教育经费的投入，2016年投入6000万元，2018年投入8640万元．假设这两年淮安投入教育经费的年平均增长率相同．
（1）求这两年淮安投入教育经费的年平均增长率；
（2）若淮安教育经费的投入还将维持相同的年平均增长率，请你预算2019年宜兴投入教育经费多少万元．
24. 如图，AB是半圆O的直径，C、D是半圆O上的两点，且OD∥BC，OD与AC交于点E。
（1）若∠B=
,求弧CD的度数；
（2）若AB=26，DE=8，求AC的长。
参考答案
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | C | B | B | C | B | A | D | A | D | D |
11. ______________________________ 12．=0__________
13．____________________________________________________________ 14．____________________________________________________________
15．__________ 16．________________________________________________________________________________
17．__________ 18．__________________________________________________________________________________________
19.
（1）2=4·····1分 ；1—x=±2···· x1=—1 x2=3·
（2）⊿=10····· ；x1= x2= ··
（3）x2-3x+=
····x-
=±
···x1= + x2=—
（4）x2+2x—8=0··；（x-2）=0···；x1=2 x2= —4··
（5）
=0··；（x-3）=0··2分；x1=3 x2= 4·
20.
解：∵方程有两个相等的实数根
∴⊿=0 即 
b2+8b-20=0
∴
∵b是正数，∴
在等腰△ABC中，∵a=5 ∴
∴△ABC的周长是12
21、
解：（1）证明：∵ 四边形ABCD 是平行四边形，
∴ AD∥BC．
∴ ∠CED＝∠BCF．
∵ ∠CED＋∠DCE＋∠D＝180°，∠BCF＋∠FBC＋∠F＝180°，
∴ ∠D＝180°－∠CED－∠DCE，∠F＝180°－∠BCF－∠FBC．
又∠DCE＝∠FBC，
∴ ∠D＝∠F．
（2）图中P 就是所求作的点． ··
22、.
（1）⊿＞0 k＞—1···；且k≠0··
（2）没有实数k .解得k=—2·；⊿＜0，没有实数k···
23、
解： 解：设这两年淮安投入教育经费的年平均增长率为x
6000（1+x）2=8640·
x1=20% x2= —2.2（舍）··
8640×1.2=10368·
24.
∵AB是直径
∴∠C=90，∠B=70
∴∠BAC=20·
∵OD∥BC
∴∠AOD=∠B=70∘，又OD=OA，
∴∠OAD=55∘，
∴∠DAC=35∘
∴CDˆ的度数是70∘；
∵AB=26，
∴OD=13，又DE=8
∴OE=5，
∵OD∥BC，OA=OB，
∴BC=2OE=10，
∴AC=24.·
