2019学年第一学期南模中学高二初态考
数学试题
1、填空题
1.设集合
，
，则
__________.
2.函数
的反函数是
__________.
3.函数
的概念域是__________.
4.已知向量、
满足
，则、的夹角为__________.
5.已知函数
是
上的奇函数，当
时，
，当
时，的分析式为
__________.
6.从数列
中可以找出无限项构成一个新的等比数列
，使得该新数列的各项和为
，则此数列的通项公式为__________.
7.已知
，，
，则在方向上的投影为__________.
8.三角形
中，
，
，则三角形面积为__________.
9.若均为平面单位向量且
，则
的坐标为__________.
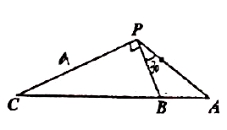
10.如图，湖面上甲、乙、丙三艘船沿着同一条直线航行，某一时刻，甲船在最前面的
点处，乙船在中间的点处，丙船在最后面的点处，且
，一架无人机在空中的
点处对它们进行数据测量，在同一时刻测得
，，则此时无人机到甲、丙两船的距离之比为__________.（船只与无人机的大小及其它原因忽视不计）
11.己知数列
的通项公式是
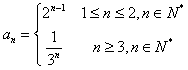，则__________.
12.函数（
）的值域为__________.
2、选择题
13.命题：“”是命题：“
”的（ ）
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既非充分又非必要条件
14.若是所在平面内一点，，则点是的（ ）
A.重心 B.垂心 C.内心 D.外心
15.若
，则一定是（ ）
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰直角三角形
16.在边长为1的正六边形
中，记以为起点，其余顶点为终点的向量分别为；以
为起点，其余顶点为终点的向量分别为
，若
分别为
的最小值、最大值，其中
，
，则满足（ ）
A.
， B.，
C.，
D.，
3、简答卷
17.已知
（为常数），且方程有两个实根为
，.
（1）求函数的分析式；
（2）当时，解关于的不等式：.
18.已知：
是同一平面内的两个向量，其中
（1）若，且与垂直，求与的夹角；
（2）若
，且与
的夹角为锐角，求实数的取值范围.
19.设正数数列的前
项和为
，对于任意，是和
的等差中项.
（1）求数列的通项公式；
（2）设，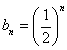
是的前项和，是不是存在常数，对任意，使
恒成立？若存在，求取值范围；若没有，说明理由.
20.设轴、轴正方向的单位向量分别为，坐标平面上的点满足条件：
，
.
（1）若数列的前项和为，且，求数列的通项公式.
（2）求向量的坐标，若
的面积
构成数列，写出数列的通项公式.
（3）若，指出为什么值时，获得最大值，并说明理由.
21.对于概念在上的函数，若函数满足：①在区间上单调递减：②存在常数
，使其值域为
，则称函数是函数的“渐近函数”.
（1）若函数，，请写出的分析式，使得是函数的“渐近函数”（不必说明理由）；
（2）判断函数是否函数
，的“渐近函数”，并说明理由；
（3）若函数，，
，求证：
是函数的“渐近函数”充要条件是
.
