![]() 上海浦东新区民办常青中学
上海浦东新区民办常青中学
初三第一学期数学期末考试题
1、选择题:(本大题共6题,每题4分,满分24分)
【每小题只有一个正确选项,在答卷纸的相应题号的选项上用2 B铅笔填涂】
1.把抛物线![]() 向右平移2个单位后得到的抛物线是( )
向右平移2个单位后得到的抛物线是( )
![]() .
.![]() ;
; ![]() .
.![]() ;
; ![]() .
.![]() ;
; ![]() .
.![]() .
.
2.在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() 的对边,下列等式中正确的是( )
的对边,下列等式中正确的是( )

![]() .
.![]() ;
; ![]() .
.![]() ;
; ![]() .
.![]() ;
; ![]() .
.![]() .
.
3.等腰直角三角形的腰长为![]() ,该三角形的重点到斜边的距离为( )
,该三角形的重点到斜边的距离为( )
![]() .
.![]() ;
; ![]() .
.![]() ;
; ![]() .
.![]() ;
; ![]() .
.![]() .
.
4.若两个相似三角形的面积之比为1:4,则它们的最大边的比是( )
![]() .1:2;
.1:2; ![]() .1:4;
.1:4; ![]() .1:5;
.1:5; ![]() .1:16.
.1:16.
5.如图,已知直线![]() ∥
∥![]() ∥
∥![]() ,直线m、n 与
,直线m、n 与![]() 、
、![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,
,![]() ,
,
![]() ,
,![]() ,则
,则![]() ( )
( )
![]() .7;
.7; ![]() .7.5;
.7.5; ![]() .8;
.8; ![]() .8.5.
.8.5.
6.在两个圆中有两条相等的弦,则下列说法正确的是( )
![]() .这两条弦所对的弦心距相等;
.这两条弦所对的弦心距相等; ![]() .这两条弦所对的圆心角相等;
.这两条弦所对的圆心角相等;
![]() .这两条弦所对的弧相等;
.这两条弦所对的弧相等; ![]() .这两条弦都被垂直于弦的半径平分.
.这两条弦都被垂直于弦的半径平分.
2、填空题:(本大题共12题,每题4分,满分48分)
【请将结果直接填入答卷纸的相应地方】
7. 二次函数![]() 图像的顶点坐标是__________.
图像的顶点坐标是__________.
8.抛物线![]()
![]() 的图像肯定经过__________象限.
的图像肯定经过__________象限.
9.抛物线![]() 的对称轴是:直线__________.
的对称轴是:直线__________.
10.已知抛物线![]() ,它的图像在对称轴__________(填“左边”或“右边”)的部分是降低的.
,它的图像在对称轴__________(填“左边”或“右边”)的部分是降低的.
11.已知![]() 、
、![]() 分别是△
分别是△![]() 的边
的边![]() 、
、![]() 的延长线上的点, 若
的延长线上的点, 若![]() ,则
,则![]() 的值是__________
的值是__________
时,![]() ∥
∥![]() .
.
12.已知线段![]() ,
,![]() ,若线段
,若线段![]() 是线段
是线段![]() 、
、![]() 的比率中项,则
的比率中项,则![]() =__________
=__________![]() .
.
13.已知三角形三边长为3、4、5,则最小角的正弦是__________.
14.在高为100米的楼顶测得地面上某十字路口的俯角为![]() ,那样楼底到这十字路口的水平距离是
,那样楼底到这十字路口的水平距离是
__________米.
15.在RtΔABC中,∠![]() ,
,![]() ,那样
,那样![]() 的值为__________.
的值为__________.
16.若⊙![]() 的一条弦长为24,弦心距为5,则⊙
的一条弦长为24,弦心距为5,则⊙![]() 的直径长为__________.
的直径长为__________.
17.如图,AB是![]() 的直径,点
的直径,点![]() 、
、![]() 在
在![]() 上,
上,![]() ,
,![]() ,则
,则![]() __________度.
__________度.
18.在![]() △
△![]() 中,∠
中,∠![]() ,
,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,且
上,且![]() ,设点
,设点![]() 关于
关于
![]() 的对称点为
的对称点为![]() ,若
,若![]() ∥
∥![]() ,则
,则![]() 的长为__________.
的长为__________.
3、解答卷:(本大题共7题,满分78分)
19.(本题满分10分)
计算:![]() .
.
20.(本题满分10分)
如图,已知![]() ,点
,点![]() 、
、![]() 、
、![]() 、
、![]() 分别在
分别在![]() 和
和![]() 上,
上,![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() ,
,![]() ,用向量
,用向量![]() 与
与![]() 表示
表示![]() .
.
21.(本题满分10分,每小题满分各5分)
如图,已知在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() .
.
(1)求证:∠![]() =∠
=∠![]() ;
;
(2)求![]() 的值.
的值.
22.(本题满分10分,第(1)小题4分,第(2)小题6分)
通过学习锐角三角比,大家了解在直角三角形中,一个锐角的大小与两条边长的比值是一一对应的,因此,两条边长的比值与角的大小之间可以相互转化。类似的,可以在等腰三角形中打造边角之间的联系。大家概念:等腰三角形中底边与腰的比叫做底角的邻对(can).
如图(1)在△![]() 中,
中,![]() ,底角
,底角![]() 的邻对记作
的邻对记作![]() ,这个时候
,这个时候![]() ,容易了解一个角的大小与这个角的邻对值也是一一对应的.依据上述角的邻对的概念解下列问题:
,容易了解一个角的大小与这个角的邻对值也是一一对应的.依据上述角的邻对的概念解下列问题:
(1)![]() =__________;
=__________;
(2)如图(2),在△![]() 中,
中,![]() ,
,![]() ,
,![]() ,求△
,求△![]() 的周长.
的周长.
23.(本题满分12分,每小题满分各6分)
如图,已知在![]() △
△![]() 中,
中,![]() ,
,![]() 于
于![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 的延长线
的延长线
与![]() 的延长线交于点
的延长线交于点![]() .
.
(1)求证:△![]() ∽△
∽△![]() ;
;
(2)求证:![]() .
.
24.(本题满分12分,每小题4分)
如图,已知直线![]() 与二次函数
与二次函数![]() 的图像交于点
的图像交于点![]() 、
、![]() ,,点
,,点![]() 为二次函数图像的顶点,
为二次函数图像的顶点,![]() ,
,![]() 的中点为
的中点为![]() .
.
(1)求二次函数的分析式;
(2)求线段![]() 的长;
的长;
(3)若射线![]() 上存在点
上存在点![]() ,使得△
,使得△![]() 与△
与△![]() 相似,求点
相似,求点![]() 的坐标.
的坐标.
25.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5分)
如图(1),已知∠![]() ,点
,点![]() 为射线
为射线![]() 上一点,且
上一点,且![]() ,
,![]() 、
、![]() 为射线
为射线![]() 和
和![]() 上的两个动点(
上的两个动点(![]() ),过点
),过点![]() 作
作![]() ⊥
⊥![]() ,垂足为点
,垂足为点![]() ,且
,且![]() ,联结
,联结![]() .
.
(1)若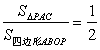 时,求
时,求![]() 的值;
的值;
(2)设![]() ,
,![]() 求
求![]() 与
与![]() 之间的函数分析式,并写出概念域;
之间的函数分析式,并写出概念域;
(3)如图,过点![]() 作
作![]() 的垂线,垂足为点
的垂线,垂足为点![]() ,交射线
,交射线![]() 于点
于点![]() ,点
,点![]() 、
、![]() 在射线
在射线![]() 和
和![]() 上运动时,探索线段
上运动时,探索线段![]() 的长是不是发生变化?若不发生变化,求出它的值。若发生变化,试用含x的代数式表示
的长是不是发生变化?若不发生变化,求出它的值。若发生变化,试用含x的代数式表示![]() 的长.
的长.
初中三年级期末调查考数学卷参考答案
一 、选择题:(本大题共8题,满分24分)
1.A ; 2.C; 3.D; 4.A; 5.B ; 6.D.
2、填空题:(本大题共12题,满分48分)
7.(0,3); 8.1、二; 9.![]() ; 10.左边;
; 10.左边;
11.![]() ; 12.12; 13.
; 12.12; 13.![]() ; 14.
; 14.![]() ;
;
15.1; 16.26; 17.40; 18.1.
3、(本大题共7题,满分78分)
19.(本题满分10分)
解:原式=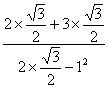 (每一个值得2分,共8分)
(每一个值得2分,共8分)
=![]() (2分)
(2分)
20.(本题满分10分,4+6)
(1)∵![]()
∴![]() . (2分)
. (2分)
∵![]() ,
,
∴![]() ∴
∴![]() . (2分)
. (2分)
(2)∵![]() ,
,![]() ,
,
∴![]() . (3分)
. (3分)
∵![]() ,
,
∴![]() =
=![]() . (3分)
. (3分)
21.(本题满分10分,每小题满分各5分)
(1)∵![]() ,
,![]() ,
,
∴∠CAB=∠BDC=90°.
∵∠AEB=∠DEC,
∴△AEB∽△DEC.
∴![]() .
.
∵∠AED=∠BEC,
∴△AED∽△BEC.
∴∠DAC=∠CBD-------------------------------------------------------------------------------
∵△AED∽△BEC ∴![]() ---------------------------------------------
---------------------------------------------
∵![]() ,
,![]() ∴
∴![]() ----------------------------------------
----------------------------------------
∴RtΔABE中,![]() =
=![]() -----------------------------------------------------------
-----------------------------------------------------------
22.(本题满分10分,第(1)小题4分,第(2)小题6分)
(1)can30°=![]() -------------------------------------------------------------------------------------(4分)
-------------------------------------------------------------------------------------(4分)
(2)∵在△ABC中, canB ![]() ,∴
,∴![]() -----------------------------------------------(1分)
-----------------------------------------------(1分)
设![]()
过点A作AH![]() 垂足为点H,
垂足为点H,
∵AB=AC ∴![]()
∵![]() ∴
∴![]()
![]() ---------------------------------------(2分)
---------------------------------------(2分)
∴![]() ---------------------------------------------------------------------(2分)
---------------------------------------------------------------------(2分)
∴△ABC的周长=![]() .----------------------------------------------------------------------------(1分)
.----------------------------------------------------------------------------(1分)
23.(本题满分12分,每小题满分各6分)
(1)∵![]() ,
,![]()
∴∠ACD+∠DCB=∠B=∠DCB=90°
∴∠ACD=∠B--------------------------------------------------------------------------------------------
∵![]() 是
是![]() 的中点 ∴DE=EC
的中点 ∴DE=EC
∴∠ACD=∠FDC
∴∠FCD=∠B-------------------------------------------------------------------------------------------
∴△FDC∽△FBD--------------------------------------------------------------------------------------
∵△FDC∽△FBD ∴![]() ----------------------------------------------------------------
----------------------------------------------------------------
∵在![]() 和
和![]() 中,
中,![]() ------------------------------------------
------------------------------------------
∴![]() -----------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------
24.(本题满分12分,每小题各4分)
∵点A在直线![]() 上,且
上,且![]() ∴A ------------------------------------------------
∴A ------------------------------------------------
∵ 点O A在![]() 的图像上,
的图像上,
∴![]() 解得:
解得:![]() ------------------------------------------------------(2分)
------------------------------------------------------(2分)
∴二次函数的分析式为![]() ---------------------------------------------------------------------
---------------------------------------------------------------------
(2)由题意得顶点P ---------------------------------------------------------------------------
∴![]()
∴![]() ∴∠AOP=90°---------------------------------------------------------
∴∠AOP=90°---------------------------------------------------------
∵∠AOP=90°,B为AP的中点 ∴![]() ------------------------------------------------
------------------------------------------------
∵∠AOP=90°,B为AP的中点
∴OB=AB ∴∠AOB=∠OAB
若△AOQ与△AOP
则①△AOP∽△OQA ∴![]() ∴
∴![]() ---------------------------------------
---------------------------------------
②△AOP∽△OAQ ∴![]()
![]() ----------------------------------------------
----------------------------------------------
∵B ∴![]() -------------------------------------------------------------------
-------------------------------------------------------------------
即点Q的坐标![]() 时,△AOQ与△AOP相似。
时,△AOQ与△AOP相似。
25.(本题满分14分,第(1)小题4分,第(2)小题5分,第(3)小题5分)
(1)∵∠ACP=∠OCB ∠CAP=∠O=90°
∴△CAP∽△COB-------------------------------------
 ∴
∴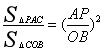 -------------------------------
-------------------------------
∵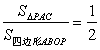 ∴
∴
∴![]()
∵AP=2 ∴![]() -------------------------
-------------------------
在Rt△OBP中, ![]() -----------------
-----------------
(2)作AE⊥PC,垂足为E,---------------------------------------------------------------------
易证△PAE∽△PCA ∴ ![]()
∴![]() ∴
∴ ![]() -------------------------------------------------------------------
-------------------------------------------------------------------
∵∠MON=∠AEC=90° ∴ AE∥OM
∴![]() ----------------------------------------------------------------------------------
----------------------------------------------------------------------------------
∴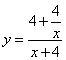 整理得
整理得![]() ------------------------------
------------------------------
(3)线段OQ的长度不会发生变化-----------------------------------------------------------
由△PAH∽△PBA 得![]() 即
即![]() ------------------------
------------------------
由△PHQ∽△POB 得![]() 即
即![]() ---------------------
---------------------
∴![]()
∵PA=2 PO=4 ∴PQ=1 ----------------------------------------------------------------
∴OQ=3--------------------------------------------------------------------------------------------------
即OQ的长度等于3。







