初一（上）数学 第9章 整式 单元测试
一．选择题（共6小题）
1．下列整式中，单项式是
A．
B．
C．
D．
2．假如长方形的长是，宽是
，则长方形的周长是
A．
B．
C．
D．
3．下列计算错误的是
A．
B．
C．
D．
4．下列多项式的乘法可以运用平方差公式计算的是
A．
B．
C．
D．
5．计算：
A．
B．
C．
D．
6．若
，则
、
的值分别是
A．2，8 B．
，
C．2， D．，8
二．填空题（共12小题）
7．计算：
__________．
8．计算：
__________．
9．计算：
__________．
10．假如单项式
与是相同种类项，那样
__________．
11．分解因式：__________．
12．已知
，
，则
__________．
13．若，则代数式
的值等于__________．
14．已知
能变形为
，则的值为__________．
15．某商品原价为元，涨价
之后，销售量降低，于是又降价
销售，则该商品现价为__________元．
16．已知一个三角形的面积为
，一条边长为，则这条边上的高为______________________________．
17．大家规定一种运算：，比如
，．根据这种运算规定，当__________时，
．
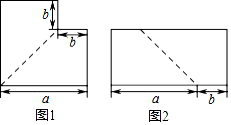
18．如图1，将边长为
的大正方形剪去一个边长为
的小正方形，再沿图中的虚线剪开，然后按图2所示进行拼接，请依据图形的面积写出一个含字母，的等式__________．
三．解答卷（共7小题）
19．计算，
．
20．因式分解：
（1）；
（2）
21．先化简，再求值：
，其中．
22．某村种植了小麦、水稻、玉米三种农作物，小麦种植面积是亩，水稻种植面积是小麦种植面积的4倍，玉米种植面积比小麦种植面积的2倍少3亩．
问：（1）水稻种植面积；（含的式子表示）
（2）水稻种植面积和玉米种植面积哪一个大？为何．
23．现概念运算“△”，对于任意有理数、，都有△
，比如：3△
，请依据上述常识解决问题：
（1）
△；
（2）若（1）的代数式值大于6而小于9，求的取值范围．
24．图①所示是边长为的大正方形中有一个边长为的小正方形．图②是由图①中阴影部分拼成的一个长方形．
（1）设图①中阴影部分的面积为
，图②中阴影部分的面积为，请用含，的式子表示：
__________，
__________；（不必化简）
（2）以上结果可以验证的乘法公式是__________；
（3）借助（2）中得到的公式，计算：
．
25．阅读下列材料：已知
，求的值．
解：，
，
依据上述材料的做法，完成下列各小题：
（1）已知
，求的值；
（2）已知，求
的值；
（3）已知，求的值．
（4）已知，求代数值
的值．
参考答案
一．选择题（共6小题）
1．下列整式中，单项式是
A． B． C． D．
解：、是多项式，不是单项式，故本选项不符合题意；
、是多项式，不是单项式，故本选项不符合题意；
、是单项式，故本选项符合题意；
、是多项式，不是单项式，故本选项不符合题意；
故选：．
2．假如长方形的长是，宽是，则长方形的周长是
A． B． C． D．
解：
长方形的长是，宽是，
长方形的周长．
故选：．
3．下列计算错误的是
A． B．
C． D．
解：、，原式计算错误，符合题意；
、，正确，不合题意；
、，正确，不合题意；
、，正确，不合题意；
故选：．
4．下列多项式的乘法可以运用平方差公式计算的是
A． B．
C． D．
解：能借助平方差公式计算的多项式的特征是：两个两项式相乘，有一项相同，另一项互为相反数．
、不可以用平方差公式进行计算，故本选项不符合题意；
、可以用平方差公式进行计算，故本选项符合题意；
、不可以用平方差公式进行计算，故本选项不符合题意；
、不可以用平方差公式进行计算，故本选项不符合题意．
故选：．
5．计算：
A． B． C． D．
解：，
，
．
故选：．
6．若，则、的值分别是
A．2，8 B．， C．2， D．，8
解：，
，
，．
故选：．
二．填空题（共12小题）
7．计算：__________
__________．
解：原式，
故答案为：．
8．计算：____________________．
解：原式．
故答案为：．
9．计算：____________________．
解：
．
故答案为：．
10．假如单项式与是相同种类项，那样______________________________．
解：单项式与是相同种类项，
，
，
．
故答案为：4．
11．分解因式：____________________．
解：原式
，
故答案为：
12．已知，，则__________
__________．
解：，
故答案为：．
13．若，则代数式的值等于______________________________．
解：，
．
．
故答案为4．
14．已知能变形为，则的值为______________________________．
解：
，
，
解得：．
故答案为：3．
15．某商品原价为元，涨价之后，销售量降低，于是又降价销售，则该商品现价为__________
__________元．
解：涨价之后的价格：，
降价后的价格：，
故答案为．
16．已知一个三角形的面积为，一条边长为，则这条边上的高为____________________．
解： 依据题意知这条边上的高为
，
故答案为：．
17．大家规定一种运算：，比如，．根据这种运算规定，当______________________________时，．
解：由题意得，
，
解得
．
故答案为：8．
18．如图1，将边长为的大正方形剪去一个边长为的小正方形，再沿图中的虚线剪开，然后按图2所示进行拼接，请依据图形的面积写出一个含字母，的等式____________________．
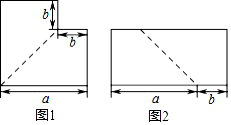
解：图1面积为，图2的面积为，
因此有：，
故答案为：．
三．解答卷（共7小题）
19．计算，．
解：原式
．
20．因式分解：
（1）；
（2）
解：（1）
（2）
21．先化简，再求值：，其中．
解：原式
，
，
原式．
22．某村种植了小麦、水稻、玉米三种农作物，小麦种植面积是亩，水稻种植面积是小麦种植面积的4倍，玉米种植面积比小麦种植面积的2倍少3亩．
问：（1）水稻种植面积；（含的式子表示）
（2）水稻种植面积和玉米种植面积哪一个大？为何．
解：（1）由题意得：水稻种植面积是；
（2）由题意得：玉米种植面积是，
，
，
水稻种植面积大．
23．现概念运算“△”，对于任意有理数、，都有△，比如：3△，请依据上述常识解决问题：
（1）△；
（2）若（1）的代数式值大于6而小于9，求的取值范围．
解：（1）△
；
（2）由题意得不等式组
解不等式①得，，
解不等式②得，
，
所以的取值范围是．
24．图①所示是边长为的大正方形中有一个边长为的小正方形．图②是由图①中阴影部分拼成的一个长方形．
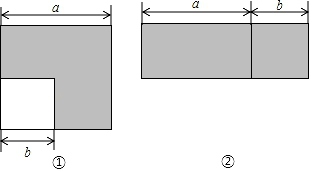
（1）设图①中阴影部分的面积为，图②中阴影部分的面积为，请用含，的式子表示：____________________，__________；（不必化简）
（2）以上结果可以验证的乘法公式是__________；
（3）借助（2）中得到的公式，计算：．
解：（1），；
（2）；
（3）
．
25．阅读下列材料：已知，求的值．
解：，
，
依据上述材料的做法，完成下列各小题：
（1）已知，求的值；
（2）已知，求的值；
（3）已知，求的值．
（4）已知，求代数值的值．
解：（1），，
答：的值为
；
（2），，，
；
答：的值为2；
（3），
设：
，，
答：的值为3999．
（4），，，
．
答：代数值的值为．
