嘉定一中高中二年级第一学期开学考数学试题
1、填空题（每题3分）
1. 在数列
中，
，且
，则________.
2. 已知
时
，则
的值为________.
3. 设
是函数
的反函数，若
，则的值为________.
4. 已知是概念域为
且
的偶函数，在区间
上是增函数，若
，则的取值范围是________.
5. 已知
为两个锐角，且
，则
的值是________.
6. 已知钝角
的终边经过点
，且，则的值为________.
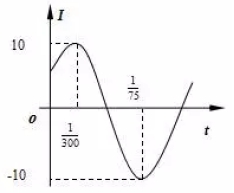7. 电流强度
（安）随时间
（秒）变化的函数的图象如图所示，则当秒时，电流强度是________安
8. 将函数
的图象向右平移
个单位后，再作关于轴对称的曲线，得到函数，则是________.
9. 函数的值域为________.
10. 曲线
和直线
在轴右边的交点按横坐标从小到大依次记为，则
等于________.
11. 
中，
、
、
分别为
、、
的对边。假如、、成等差数列，
，的面积为，那样________.
12. 已知等比数列及等差数列，其中
，公差。将这两个数列的对应项相加，得一新数列
，则等比数列的前10项之和为________.
2、选择题（每题3分）
13. 已知奇函数的概念域为，且是以2为周期的周期函数，数列是首项为1，公差为1的等差数列，则
的值为（ ）
A. 0 B. 2008 C. -2008 D. 1004
14. 已知，恒有
成立，且
，则实数
的值为（ ）
A. B. C. 或3 D. 或1
15. 已知数列的前项和为
，某三角形三边之比为，则该三角形最大角为（ ）
A. 90° B. 120° C. 135° D. 150°
16. 给定，概念使得乘积
为整数的值叫做理想数，则区间内所有理想数的和为（ ）
A. 2016 B. 2017 C. 2054 D. 2028
3、解答卷
17. （本题满分10分）已知函数是一次函数且，成等比数列，设
（1）求数列的前项和；
（2）设
，求数列的前项和
18. （本题满分10分）已知
（1）求的值
（2）求函数的最大值
19. （本题满分10分）已知奇函数的概念域为，且在区间
上是增函数，问是不是存在这种实数，使得
对所有些均成立？若存在，求出所有合适条件的实数；若没有，试说明理由。
20. （本题满分10分）假设A型进口车关税税率在2002年是100%，在2007年是25%，2002年A型进口车每辆价格为64万元（其中含32万元关税税款）
（1）已知与A型车性能相近的B型国产车，2002年每辆价格为46万元，若A型车的价格只受关税减少的影响，为了保证2007年B型车的价格不高于A型车价格的90%，B型车价格要逐年减低，问平均每年至少降低多少万元？
（2）某人在2002年将33万元存入银行，假设银行扣利息税后的年利率为1.8%（5年内不变），且每年按复利计算（上一年的利息计入第二年的本金），那样5年到期时这笔钱连本带息是不是肯定够买按（1）中所述降价后的B型车一辆？
21. （本题满分12分）如图，下面的表格内的数值填写规则如下：先将第1行的所有空格填上1；再把一个首项为1，公比为
的数列依次填入第一列的空格内；其它空格根据“任意一格的数是它上面一格的数与它左侧一格的数之和”的规则填写
| 第1列 | 第2列 | 第3列 | … | 第 |
第1行 | 1 | 1 | 1 | … | 1 |
第2行 |
|
|
|
|
|
第3行 |
|
|
|
|
|
… | … |
|
|
|
|
第 |
|
|
|
|
|
（1）设第2行的数依次为
，试用表示
的值；
（2）设第3列的数依次为
，求证：对于任意非零实数，；
（3）能否找到的值，使得（2）中的数列的前项成为等比数列？若能找到，的值有多少个？若不可以找到，说明理由。
参考答案
1、填空题
1. 8 2. 0 3. 3 4. 
5. 
6. 
7. 5 8. 9. 10. 11. 
12. 1023
2、选择题
13. A 14. D 15. B 16. D
3、解答卷
17. （1）； （2）
18. （1）1； （2）
19. 存在，
20. （1）2万元； （2）够买
21. （1）
； （2）证明略； （3）当且仅当且时，
数列
是等比数列
