永昌学校第一学期初二第二次调查
数学试题
（时间：
100分钟 满值：
100分） 2019.12
选择题（本大题共6小题，每小题3分，共18分）
1.下列命题中真命题的是（ ）
（A）三角形的外角等于三角形的两个内角和
（B）两个全等三角形对应边上的中线相等
（C）三角形的一个外角大于每个内角
（D）面积相等的两个三角形肯定是全等三角形 第2题图
2.△ABC中,∠C=90°,CD是AB上的中线,CE是AB上的高,下列判断正确的有（ ）
①∠B=∠1; ②∠1=∠3; ③∠2=∠3; ④∠A+∠B=90°
（A）①②④ （B）①③④ （C）①②③ （D）②③④
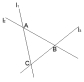3.如图,三条相互交叉的公路交于A、B、C三点,现要建一个货物中转站,需要它到三条公路的距离相等,则可供选择的地址是△ABC的（ ）
（A）三边高的交点 （B）三边中垂线交点
（C）三边中线交点 （D）三内角平分线交点
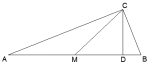
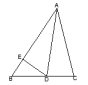
4.如图在△ABC中,∠ACB=90°,CD⊥AB,M是AB的中点,若CM=2CD,则下列结论中错误的是（ ）
（A）CB=
AB （B）CD=
MD
（C）∠BCM=75° （D）∠ACM=15°
5.如图Rt△ABC中∠ACB=90°,将它折叠使点A落在边BC的点A’处,折痕为CD,若∠A’DB=20°,则∠B=（ ）
（A）45°
（B）35°
（C）30°
（D）40°
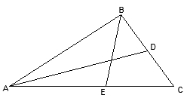
6.AD、BE是△ABC中的角平分线,分别交BC、AC于D、E,若AD=AB,BE=BC,则∠C的度数是（ ）
（A）69°
（B）
°
（C）
°
（D）不可以确定
填空题（本大题共12小题，每小题3分，共36分）
7.直角三角形中,两锐角的平分线相交所成的说角度数是__________° ；
8.如图,在△ABC中,AB=10,AC=8,∠BAC=45°,AD是∠BAC的平分线,
DE⊥AB于点E,则DE的长是__________；
9.在国内沿海有一艘不明国籍的轮船进入国内海域,我海军甲乙两艘巡逻艇立即从相距13海里的
A、B两基地前去拦截,6分钟后同时到达C地成功将它拦截,已知甲巡逻艇每小时航行120海里,
乙巡逻艇每小时航行50海里,航向为北偏西40°,则甲巡逻艇航向为北偏东__________° ；
10.△ABC的三边AB、BC、CA分别长20、30、40,其三条角平分线相交于O点,将△ABC分为三个三角形,则S△ABO:S△BCO:S△CAO =__________;
11.在△ABC中,AB=15,AC=13,边BC上的高AD=12,则△ABC的周长为__________;
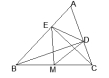
12.如图,已知BD、CE是△ABC的高,M是BC边上的中点,若△EMD
是等腰直角三角形,则∠A=__________° ；
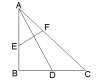
13.如下左图在△ABC中∠C=90°,斜边AB的中垂线分别交AC、AB
于E、F,若∠A=
,则∠CBE=__________° ；
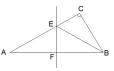
14.如下中图,在Rt△ABC中,∠B=90°,AB=BC,AD是BC边上
的中线,EF是AD的垂直平分线,交AB于点E,交AC于点F,
求AE:BE =__________;
15.如图,在平面直角坐标系中,面积为100的正方形ABCD的两个顶点
A、B在坐标轴上滑动,点B由原点O出发沿x轴正方向移动,点A
沿y轴正半轴向原点O移动,当∠ABO=36°时,边AB的中点E经过
的路径长是__________;
16.等腰△ABC中AB=AC,已知AB的垂直平分线DE交直线AC于E,垂足为D,
若DE与AC所夹的锐角是37°,则该等腰三角形的顶角度数为__________;
17.已知△ABC中,AB=AC, ∠A=40°,O为边BC的中点,把△ABC绕O顺时针旋转m（0＜m＜180）度后,假如点B恰好落在初始△ABC的边上,那样m=__________;
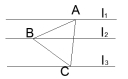
18.如图所示，l1∥l2∥l3，l1、l2间的距离为3, l2、l3间的距离为6,
等边△ABC三个顶点均在l1、l2、l3上，则△ABC的边长为__________。
简答卷（4+5+5，共14分）
19.如图，已知∠MON及线段a，点G是射线ON上的点，
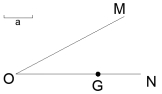求作:点P，使点P到OM、ON的距离相等，且PG=a。
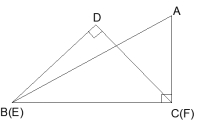
20,已知一副三角尺如图放置，把Rt△DEF沿边BC向右移动，设AC=a cm,当点D移动到边AB上时。
求: BE的长。
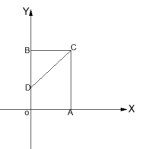
21.如图在直角坐标平面系中,矩形OACB的顶点O在坐标原点，A 、B,
已知: OB边上有一点D。若DE⊥CD于D交x轴于E,请求出点E的坐标。
证明题（6+8+8，共22分）
22.如图，已知AE⊥BD于点E，CF⊥BD于点F，AD=BC，BE=DF，AC交BD于G，
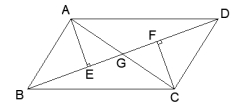求证：AG=CG。
23.如图，已知△ABC中，CD⊥AB于D，AE是边BC上的中线，要证明∠B=2∠EAB需增加一个条件，写出这个条件是__________
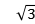且加以证明：
__________
__________
__________
__________
__________
__________
__________
__________
__________
__________
__________
24. 如图，在△ABC中，AB=2AC, 点D在BC上，且∠CAD=∠B，点E是AB的中点，联结CE与AD交于点G,点F在BC上，且∠CEF=∠BAC.
若∠BAC=90°,如图1,求证: EG+ EF=AC;
若∠BAC=120°,如图2,请猜想线段EG，EF和AC之间的数目关系并证明.
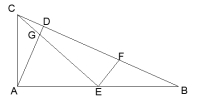
图1 图2
综合题（共10分）
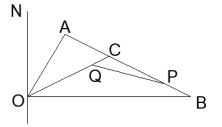
25. 已知:如图在Rt△ABC中，∠A=90°，∠AOB=60°，0B=2， ∠AOB的平分线0C交AB于C，过O点作与OB垂直的直线ON.动点P从点B出发沿折线BC-CO以每秒1个单位长度的速度向终点O运动，运动时间为t秒，同时动点Q从点C出发沿折线CO-ON以相同的速度运动，当点P到达点O时P、Q同时停止运动.
求OC、BC的长;
设△CPQ的面积为S,求S与t的函数关系式
当P在OC上、Q在ON上运动时，设PQ与OA交于点M,当t为什么值时，△OPM是等腰三角形?请求出所有满足条件的t的值。
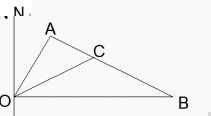
图（1） 图（2） 备用图
